All posts by Valerio Marra
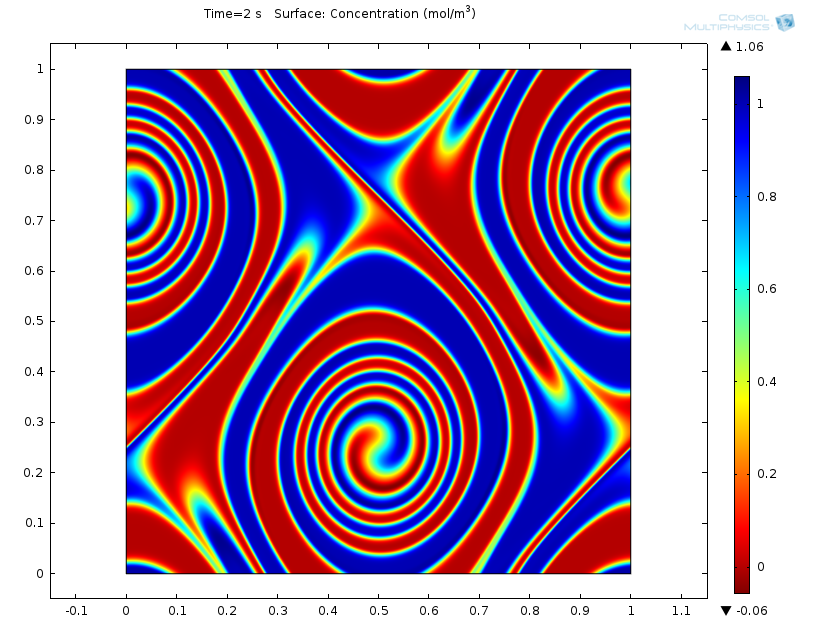
Simulating Kelvin-Helmholtz Instability and Climate Dynamics
Q: What do heated soap bubbles, wavy clouds, and Jupiter’s Great Red Spot have in common? A. An unstable motion called Kelvin-Helmholtz instability.
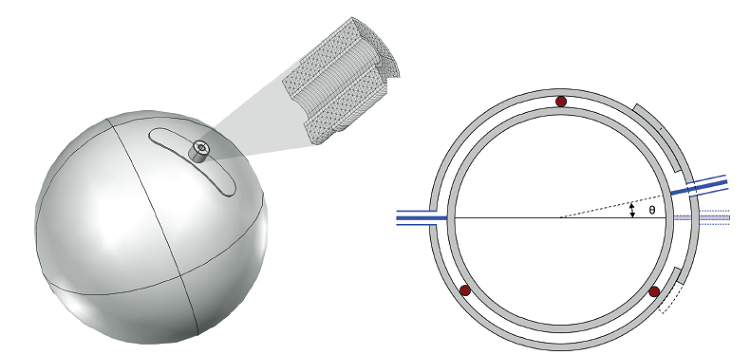
Perfect Imaging, From Theory to Reality via Simulations
Perfect imaging refers to the idea of producing images with details below the diffraction limit, where even the smallest elements can be resolved to unlimited sharpness regardless of the wavelength of light being used. While just a theory 150 years ago, research has brought us closer to reality over the years. Now, by way of simulation, researchers at Cedint Polytechnic University of Madrid in Spain are taking it one step further.
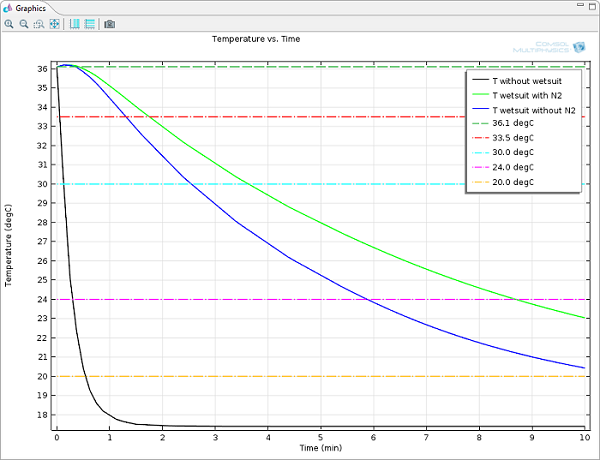
Thermal Insulation with Bubbles is Better
As a nuclear engineer, I’ve attended many thermal engineering classes. Whereas I’ve enjoyed learning techniques to enhance heat transfer, I’ve also found fascinating those applications where it is important to reduce heat transfer using the right choice and combination of materials and shapes. The design of this is vital for many industries, including the building and aerospace industries. Lately, I came across an interesting example of thermal insulation in the most mundane of these things: clothing design. I had to […]
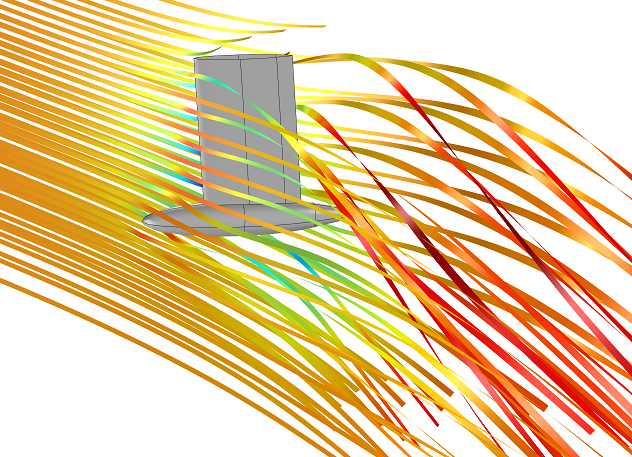
The Physics of Sailing, a CFD Analysis
Of all boats, I find sailboats to be the most fascinating, especially when sails are their only means of propulsion. Kinetic energy is transferred from the wind to the sails, which results in a lift force that balances drag forces and allows the sailboat to move through the water. We are all familiar with the parts of a boat above the waterline: deck, spars, sails, and the rudder used to turn the boat (figure 1c). Not everyone pays attention to […]
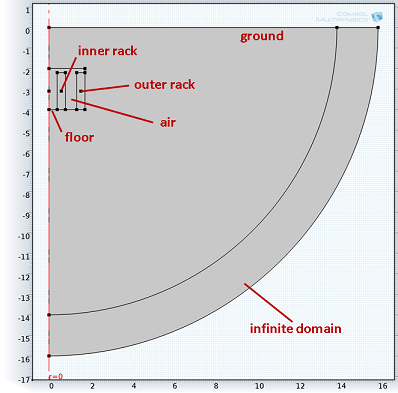
Modeling Temperature of a Wine Cellar
A lot of effort is put into inventing or improving existing technologies used to cool buildings, food, or any goods that need to be stored at a definite temperature. The reason is simple: adopting more efficient designs will result in achieving the same goal while consuming less energy. Both our balance sheet and the environment will benefit from these solutions. Here we will explore modeling temperature of a passive cooling design using a wine cellar as an example.

Optimal Distribution: Tree Roots and Microreactors
I love trees and my favorite is definitely the ficus, all varieties included. A few weeks ago I had the chance to admire a stately ficus microcarpa (see figure below). What struck me above all were its aerial roots. Roots are designed to absorb water and nutrients, sustaining the tree and synthesizing substances responsible for its growth. A thought crossed my mind right away: the shape of those roots and the way they coalesce have surely been optimized by Mother […]

When Marshmallows Become Rock-hard
A while back, I bought a bag of marshmallows, indulged a bit, and then forgot about the opened bag for a few weeks. To my surprise, and disappointment, when my marshmallows cravings returned the top ones were rock-hard while the bottom ones were almost as soft as when I bought them. Why was this the case? By leaving the bag open, water had migrated from the marshmallows into the air.
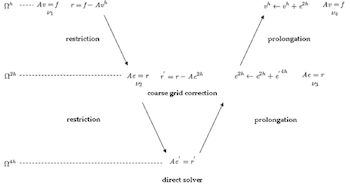
On Solvers: The V-Cycle Multigrid
As discussed previously on the blog, iterative methods efficiently eliminate oscillatory error components while leaving the smooth ones almost untouched (smoothing property). Multigrid methods, in particular, use the smoothing property, nested iteration, and residual correction to optimize convergence. Before putting all of the pieces of this proverbial puzzle together, we need to introduce residual correction and dive a bit deeper into nested iteration. Let’s begin with the latter of these elements.
