You can use the new Schrödinger Equation interface for modeling with the Semiconductor Module in the latest release of the COMSOL® software. Let’s look at a simple example model that uses this interface to estimate the electron and hole ground state energy levels for a superlattice structure. By building models like this one, device engineers are able to calculate the band gap for a given periodic structure and adjust the design parameters until a desired band gap value is achieved.
Editor’s note: This blog post was updated on 1/23/2020 to reflect new functionality and information.
The Effective Band Gap of a Superlattice Structure
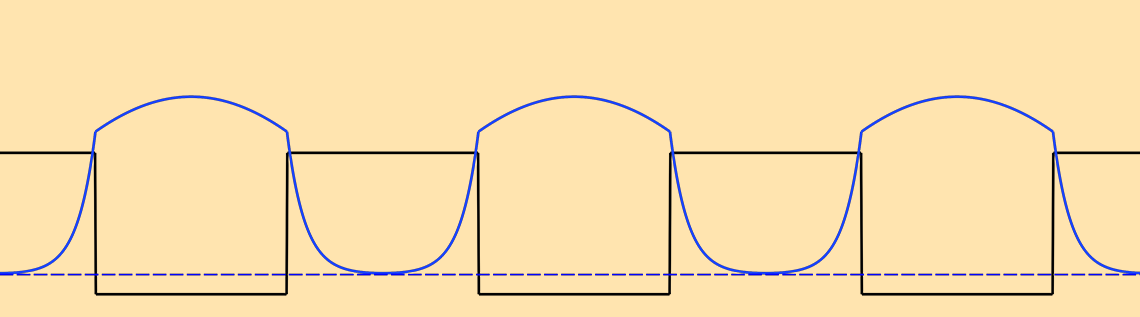
The effective band gap of a superlattice structure is wider than the one in the bulk well material, because of the quantum confinement effect — electrons and holes are mostly confined in the wells with their ground-state energies shifted away from the band edges. An example is shown below, where the black and gray lines show the conduction and valance band edges, and blue and green curves show the electron and hole wave functions shifted by the ground state energies, respectively.
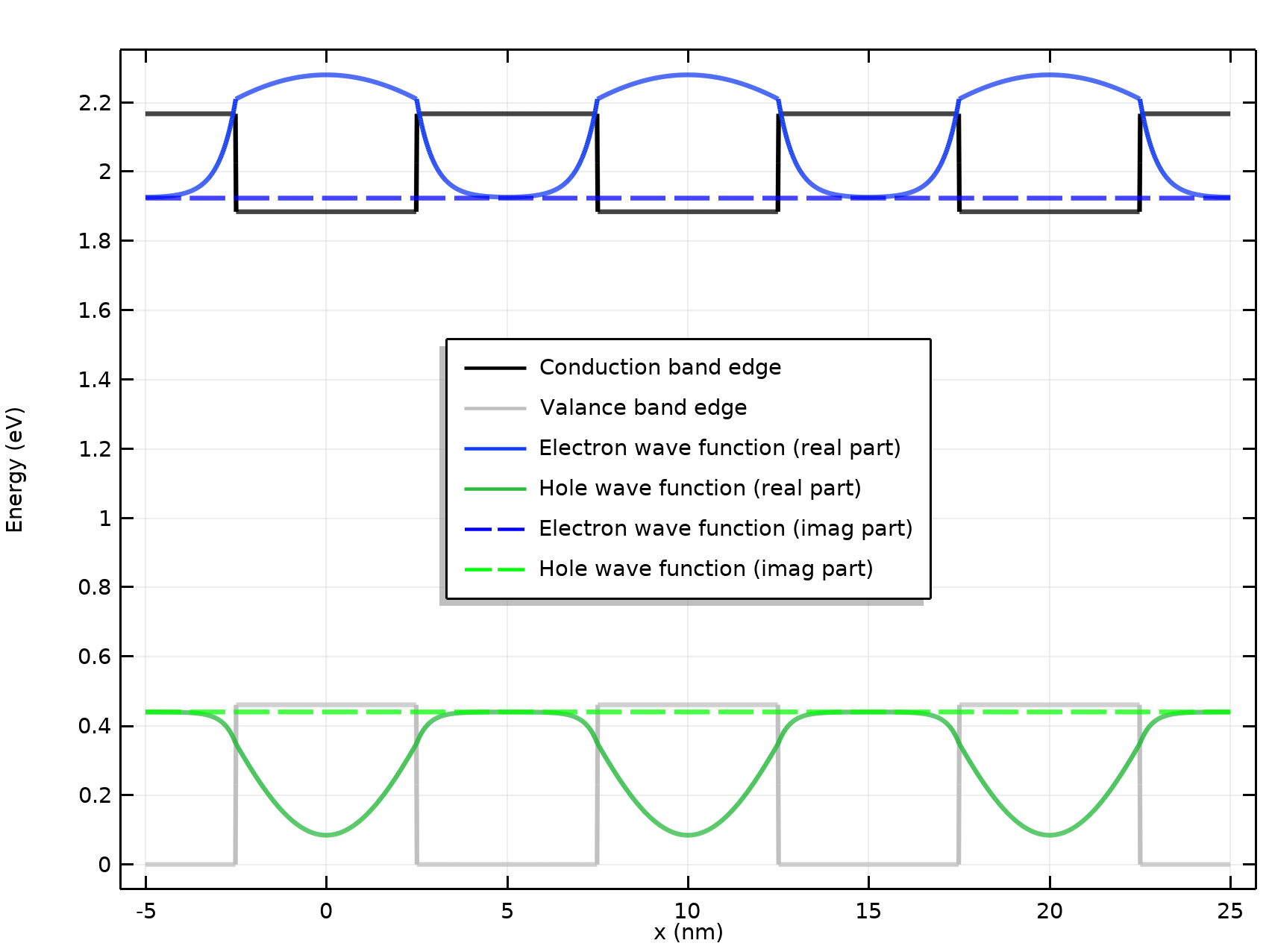
Summary graph of the superlattice band gap model.
The COMSOL Multiphysics® Model
The model is straightforward and easy to understand. Two Schrödinger Equation interfaces are used: one for electrons and the other for holes. Under each interface, two Electron Potential Energy nodes are used to set up the square-wave-shaped band edge and similarly, two Effective Mass nodes are used to set up the effective masses in the well and barrier regions. Only one unit cell of the superlattice structure needs to be included in the model, with the endpoints assigned to the Periodic Condition boundary condition.
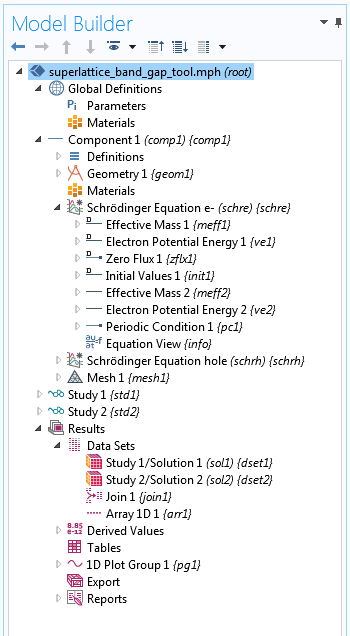
The Model Builder tree structure.
The ground state energies of the electrons and holes are solved separately in two eigenvalue studies. The result is extended from one to three unit cells using the Array 1D data set, which is also new in version 5.3 of the COMSOL Multiphysics® software.
About the Schrödinger Equation Interface
There are some parameters in the Settings pane of the physics interface worth noting.
The Settings pane for the Schrödinger Equation interface.
Eigenvalue Scale
One important parameter is the eigenvalue scale λscale (unit: J). This parameter is used for eigenvalue studies to scale the unitless eigenvalue relative to the eigenenergy. For example, the default value of 1 eV allows the numerical value of the eigenvalue to take on the value of the eigenenergy in units of eV. Therefore, the eigenvalue of 1.924, shown in the screenshot below, corresponds to the eigenenergy of 1.924 eV.
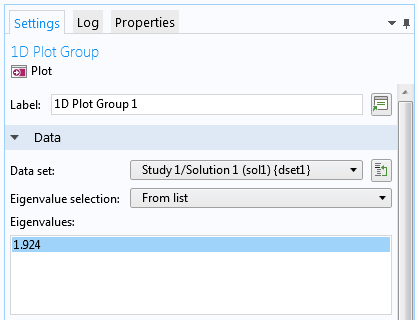
The settings for the eigenvalue study.
If the eigenvalue scale is set to 1 meV instead, then the same eigenvalue would correspond to the eigenenergy of 1.924 meV (as a result from a different model).
Energy
Another parameter is the energy E (unit: J), used for stationary studies to specify the total energy for the stationary Schrödinger equation.
Sign Conventions in the Schrödinger Equation Interface
Time-Harmonic Factor
The single-component Schrödinger equation implemented in the physics interface reads:
Note that the energy operator on the right-hand side of the equation takes an opposite sign convention as the one adopted in most textbooks of quantum mechanics. This is because COMSOL Multiphysics takes the engineering convention of exp(+iωt) for time-harmonic solutions, as opposed to the physics convention of exp(–iωt). The engineering convention is adopted for the Schrödinger Equation interface so that the sign convention is consistent within the COMSOL® product suite. Under this unusual sign convention, the momentum operator also acquires an opposite sign — since a plane wave is now exp(–ikx + iωt), and not exp(+ikx – iωt), as in most textbooks.
Electron Potential Energy
The sign convention for the Electron Potential Energy domain condition follows the one adopted by the Semiconductor interface. For electron-like particles, the direction of lower energy is in the negative direction of the electron potential energy. Pictorially, this type of particle tends to fall down to the bottom of an electron potential energy well. For hole-like particles, the direction of lower energy is in the positive direction of the electron potential energy. This type of particles tends to float up to the top of an electron potential energy peak pictorially.
Another Example of the Schrödinger Equation Interface
The Double Barrier 1D benchmark model also uses the Schrödinger Equation interface. It includes a number of different ways of applying this physics interface, such as:
- Eigenvalue study of the quasibound states
- Transient study of the decay of the quasibound states
- Eigenvalue study to solve for the resonant tunneling condition, where a 100% transmission occurs in the classically forbidden region — a peculiar, purely quantum mechanical effect
- Stationary study to solve for the transmission and reflection coefficients as a function of energy, showing narrow transmission peaks centered around the resonant tunneling energies
For this model, the Open Boundary boundary condition is used to allow the wave function to leak out of the modeling domain without reflecting back. This boundary condition also has an optional Incoming wave feature and an advanced physics option of Incoming type for the resonant tunneling condition, where 100% of the wave function is injected into the modeling domain without reflecting back out.
We hope to see more applications of this new physics interface by our users, for both general quantum mechanics problems as well as for quantum wells, wires, and dots.
Further Resources
- Learn more about new features in the Semiconductor Module with COMSOL® software version 5.3 in the Release Highlights
- Browse more examples of semiconductor simulation on the COMSOL Blog:





Comments (9)
峰 程
May 31, 2017Amazing…
Is it an ab initio method or semiclassical method?
Can I change the shape of barrier or truncate the period at a point or boundary?
Chien Liu
June 1, 2017Dear 峰, Thank you for the comments.
No we are not looking at the microstructure of the superlattice, we just take the envelope function approximation to solve a simple Schrodinger Equation for a particle in a square wave potential given by the bulk band edges as shown in the screenshot.
Yes you can specify any arbitrary potential profile – just enter a math expression in terms of the spatial coordinates x, y, and/or z in the input field.
If the structure has a finite number of periods, then we can’t use the periodic boundary condition and need to include the entire structure in the model.
Sincerely,
Chien
Edwin Vargas
May 6, 2018Dear Chien Liu,
Nice work!
Can the COMSOL module solve time depending Schrödinger Equations?
Best regards,
Edwin.
Chien Liu
May 6, 2018Dear Edwin, Thank you and yes time dependent study is supported. Please see this example:
https://www.comsol.com/model/double-barrier-1d-47041
Sincerely, Chien
HuiWen Cheng
February 10, 2020Hello Chien Liu:
Could this model be applied to type-II band alignment superlattices?
Because this example is quantum well with type-I band alignment.
Thanks.
Sincerely, Grace
Chien Liu
February 10, 2020 COMSOL EmployeeDear HuiWen, Yes you should be able to model type-II alignment using similar techniques. Sincerely, Chien
HuiWen Cheng
February 12, 2020Dear Chien Liu: I had made the .mph for type-II superlattice. However, there are some error after computing. Could I attach .mph file tofurther check the problem? Thanks.Sincerely, HuiWen
Chien Liu
February 12, 2020 COMSOL EmployeeHi HuiWen, Please contact support@comsol.com for additional assistance with your modeling problem. Sincerely, Chien
HuiWen Cheng
February 19, 2020Dear Chien Liu: Thank you. Sincerely, Huiwen