
As the capabilities and resolution of additive manufacturing technologies continue to improve, it will be possible to develop lightweight, lattice cell configurations with fine-enough microgeometries that offer optimal sound absorption properties across a very broad frequency range. The prospect of designing potential “virtual” microgeometry design configurations using numerical simulation techniques and then printing them, without being constrained by what can traditionally be manufactured and tested, is indeed very exciting.
The design strategies for both optimum sound absorption performance and broadband sound absorption performance of the lattice cells are presented in this blog post, based on natural extensions of numerical prediction methods developed for fibrous and open-cell foam acoustic materials.
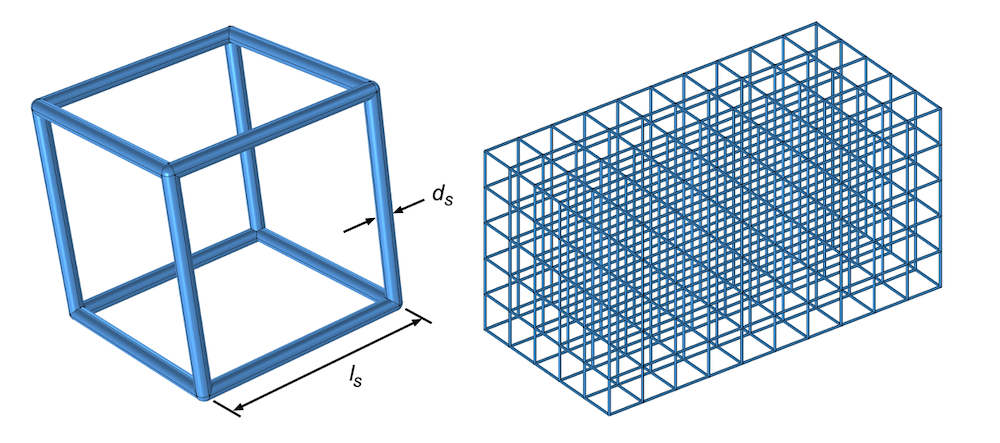
Figure 1: Conceptual unit lattice cell geometry as part of a regular array of lattice cells, defined in terms of strut diameter, d_s, and strut length, l_s.
COMSOL Multiphysics® as a Virtual Laboratory to Support Model Development
In our recent work developing analytical poroelastic acoustic models of fibrous insulation blankets and open-cell foams (Ref. 1–2), the materials considered had been produced using traditional manufacturing techniques: fiber spinning and air laying for the fibrous materials and chemical reaction processes for the foam materials.
The key physical dynamic viscous dissipation and oscillatory heat transfer mechanisms included in these models had not yet been researched extensively in the acoustics community, so it was very difficult to imagine a set of experiments on these typically inhomogeneous materials, which could decisively validate the theoretical assumptions of the models.
The thermoviscous acoustics and heat transfer modeling capabilities of the COMSOL Multiphysics® software were then utilized as a virtual laboratory, providing a set of numerical experiments to help understand the viscous fluid dissipation and oscillatory heat transfer mechanisms of the underlying assumed cylindrical fiber and foam strut geometries in the porous materials.
The starting point was working with simple 2D models of cylindrical cross sections, eventually becoming complex 3D fiber arrays and foam geometries, which ultimately leads to the successful prediction and comparison with measurement of the macroscopic acoustic performance of the fibrous and foam materials.
An important benefit of these numerical experiments was the ability to understand physical behavior at micro- and even nanometer scales. Dynamic viscous dissipation strength within fluid boundary layers, and the thermal fields within the solid fibers or foam cell struts could be explored extensively within the virtual laboratory for a variety of fluid and solid constitutive material properties, and cell microgeometries. It was observed that extremely fine diameter struts or fibers provided very high viscous losses in the fluid, occurring within the boundary layer near the solid–fluid interface (Figures 2 and 3).
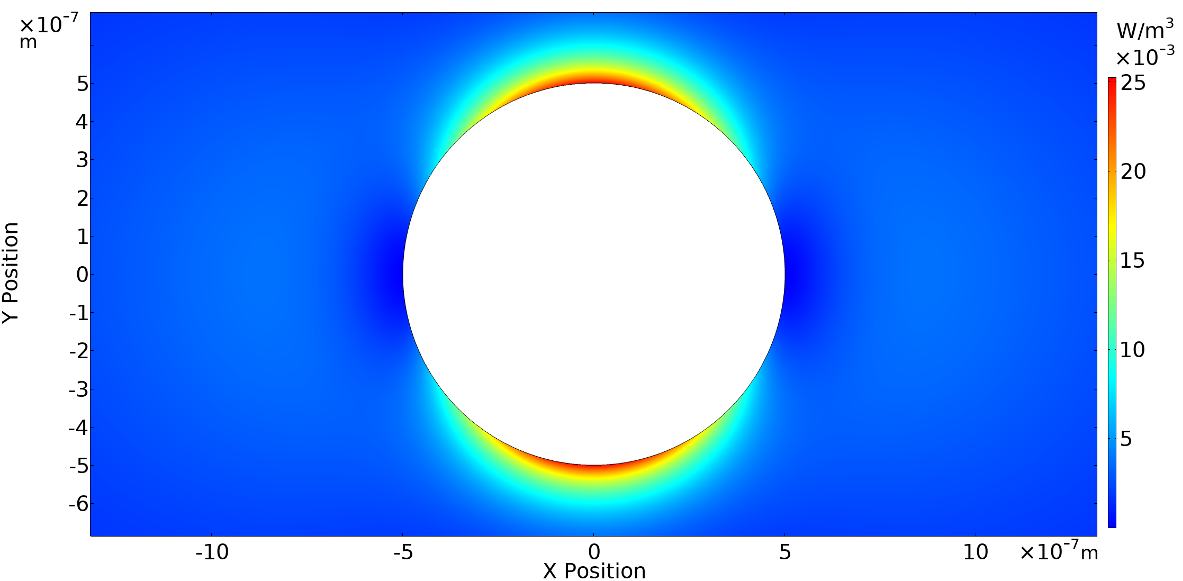
Figure 2: Viscous power dissipation density contours surrounding a cylindrical strut at 1000 Hz.
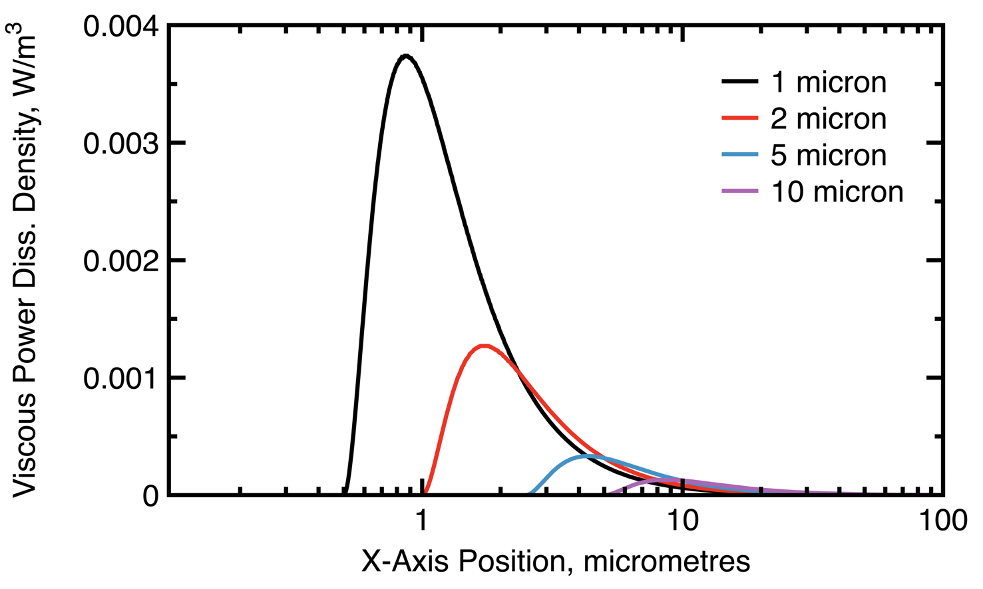
Figure 3: Viscous power dissipation densities at 1000 Hz for strut diameters of 1, 2, 5, and 10 micrometers.
It was also observed that depending on the thermal conductivity of the solid fiber or strut material, and the diameter, the thermal field within the solid will also dynamically couple with the thermal field in the surrounding fluid, in turn influencing sound wave propagation through the porous material at relevant frequencies (Figures 4 and 5).
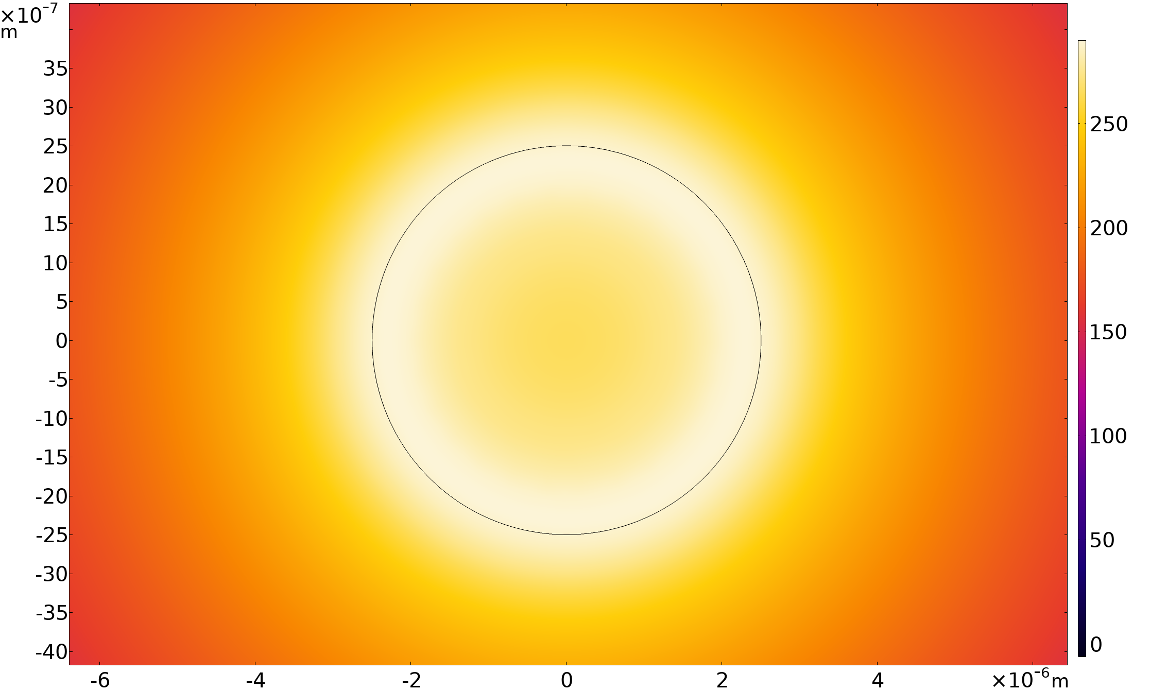
Figure 4: Thermal field contours (K) within the cylindrical strut and the surrounding thermoviscous fluid.
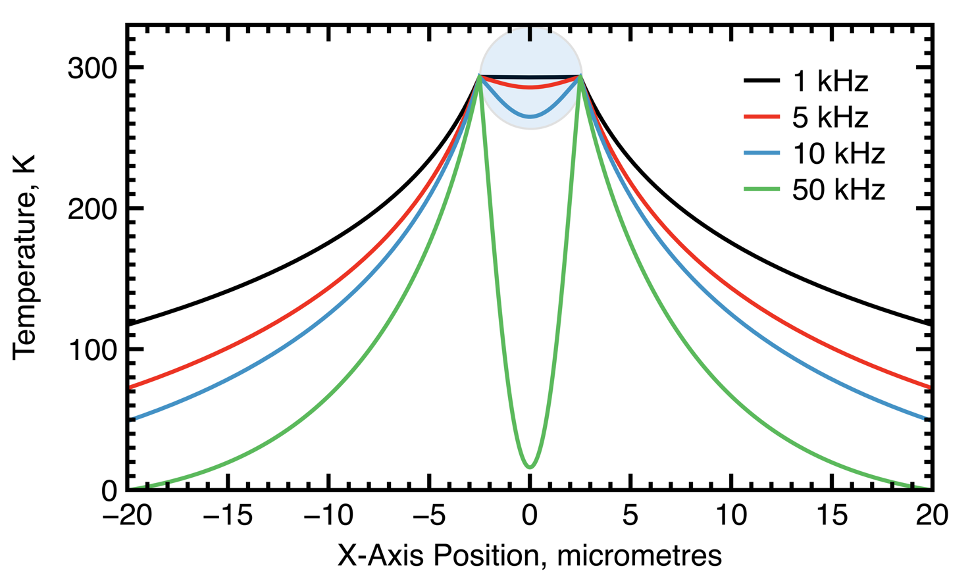
Figure 5: Temperature profile (K) across the cylindrical strut and thermoviscous fluid for 1, 5, 10, and 50 kHz frequencies.
Through this learning process, we have identified the physical clues enabling the development of optimum lightweight microstructures for sound absorption performance, even in elevated temperature conditions. With the extension of the modeling approach toward additively manufactured lattice-cell microstructures, we can also take advantage of the continuous improvements in printing technologies to begin to realize “design to print” optimized microstructural designs that achieve either near-perfect sound absorption at the quarter-wavelength frequency for a given layer thickness, or a broad, high-sound absorption performance from low to high frequencies with minimal material usage. This latter point is of special interest, given space restrictions in many industrial applications.
Acoustic Modeling of Lattice Structures
The microgeometries of additively manufactured lattice cells are often regular, repeating structures, with struts connecting between the joints of the cells, as shown in Figures 1 and 2. It is then possible to model the acoustics of individual cells, and project wave propagation behavior throughout an array of cells.
A practical approach for efficient design is to use analytical models for dynamic viscous dissipation and thermal impedance at the fluid–solid interfaces within an acoustic transfer matrix model (TMM) of wave propagation through the porous material (Ref. 1–2). For more complex cell geometries, where an analytical approach cannot be used, the viscous dissipation and thermal impedances for the single cell may also be estimated directly within COMSOL Multiphysics using 3D finite elements and then incorporated within the TMM wave propagation model through the cell array. This is the most general approach but has the drawback of currently being very computationally intensive.
As part of a typical verification process of the analytical model development for the unit cell shown in Figure 1, the dynamic viscous drag force impedances are estimated for the individual struts and their contributions combined to provide a result for the complete cell. This is then compared to a 3D finite element COMSOL Multiphysics thermoviscous acoustics model (TVA) of the complete cell (Figures 6 and 7), where for a lattice cell design having high viscous dissipation impedance (strut diameter of 5 micrometers and strut length of 70 micrometers), the analytical result of 53305 Ns/m4 compares to the 3D TVA result 54247 Ns/m4 within 2% at the almost quasistatic frequency of 0.01 Hz.
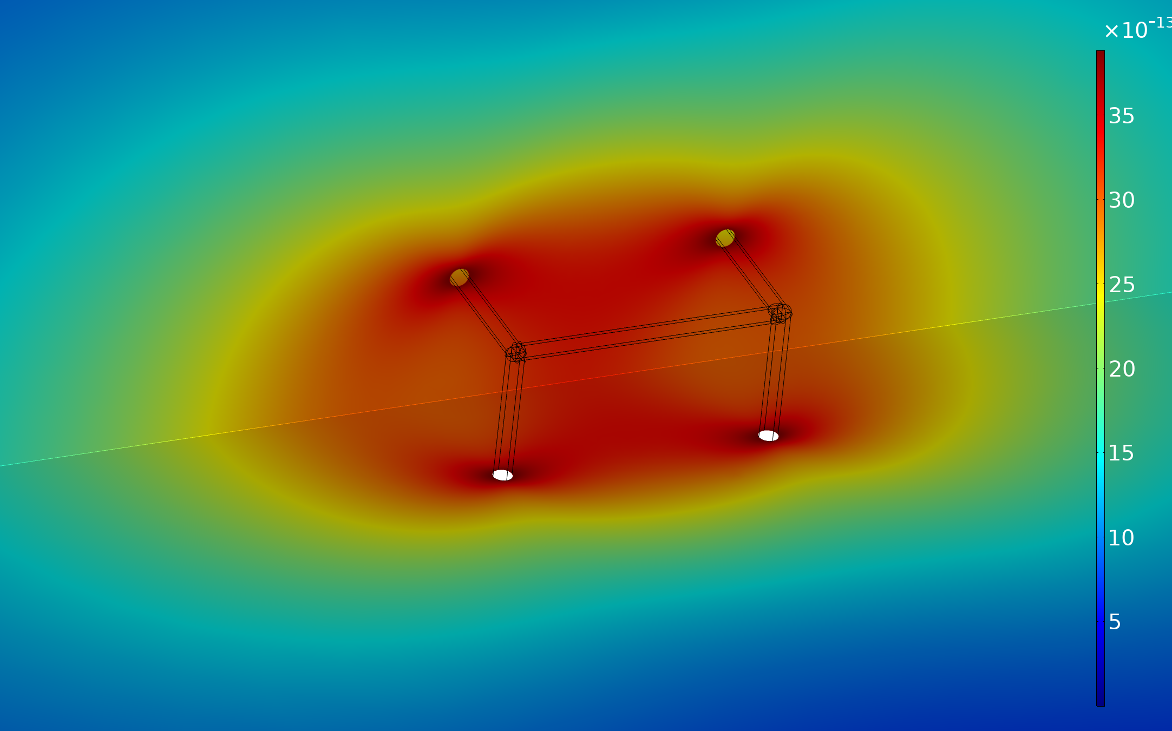
Figure 6: Fluid velocity field (m/s) surrounding the lattice cell struts at 0.01 Hz.
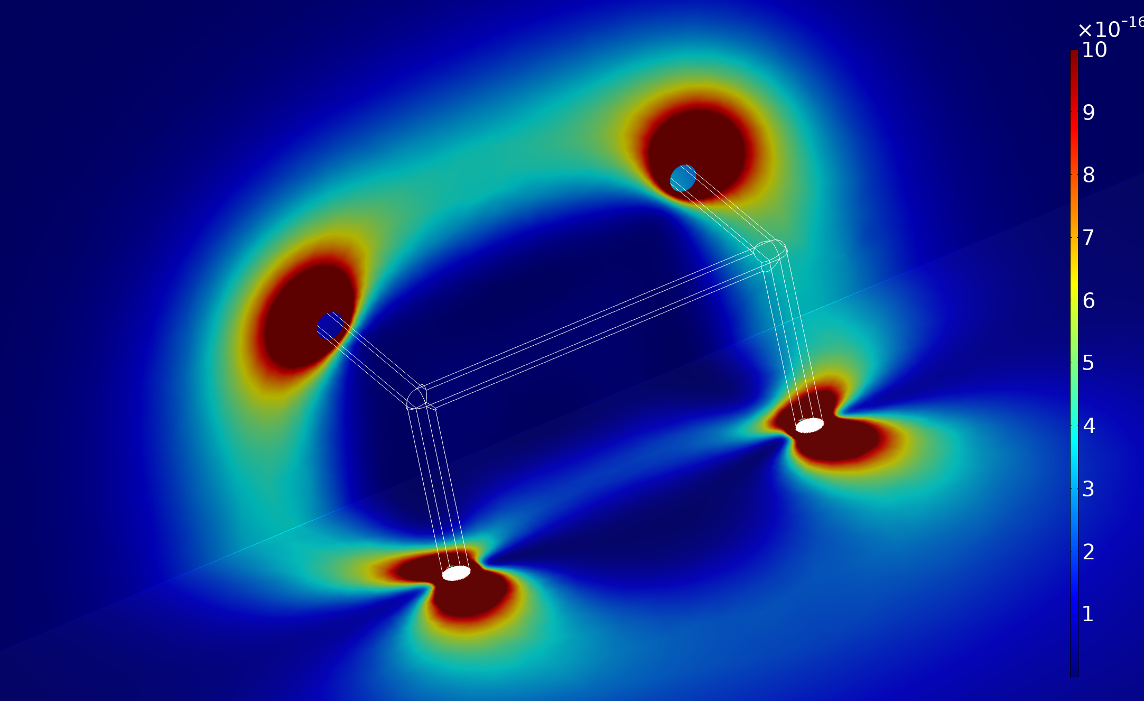
Figure 7: Fluid viscous power dissipation density (W/m3) surrounding the lattice cell struts at 0.01 Hz.
Having confidence in our analytical models, we can continue with exploring the design of the lattice cells in terms of sound absorption performance.
Perfect and Broadband Sound Absorption Optimization
To optimize the sound absorption behavior of additively manufactured lattice cells through the definition of strut diameters, strut lengths, or cell porosities, the ISO-defined surface average absorption (SAA) quantity is chosen as the performance target. It is specified as the sound absorption average for the octave band frequencies from 200 to 2500 Hz, such that large values of SAA yield high sound absorption levels across a broad frequency range, especially at low frequencies.
Taking advantage of the numerical efficiency of the lattice cell acoustic TMM, we can run a series of simulations over a range of cell dimensions (porosities) and strut diameters to map out the SAA design sensitivity for a variety of lattice-cell arrays at given thicknesses, as shown in Figures 8 and 9. Note that in these contour maps, the very definition of SAA implies that higher levels indicate a cell design that achieves elevated levels of sound absorption across a very broad frequency range. Note that once the desired lattice cell porosity and strut diameters are chosen from the SAA contour map, the strut length is then related by l_s=\sqrt{(3/4)\pi d_s^2/(1-\phi)}, where \phi is the cell porosity, or the volume of fluid per unit cell volume.
Creating these contour maps for numerous layer thicknesses then provides a very good design starting point for optimizing additively manufactured lattice cells for sound absorption behavior, especially highlighting which cell designs to target or neglect within the resolution limits of the printing process.
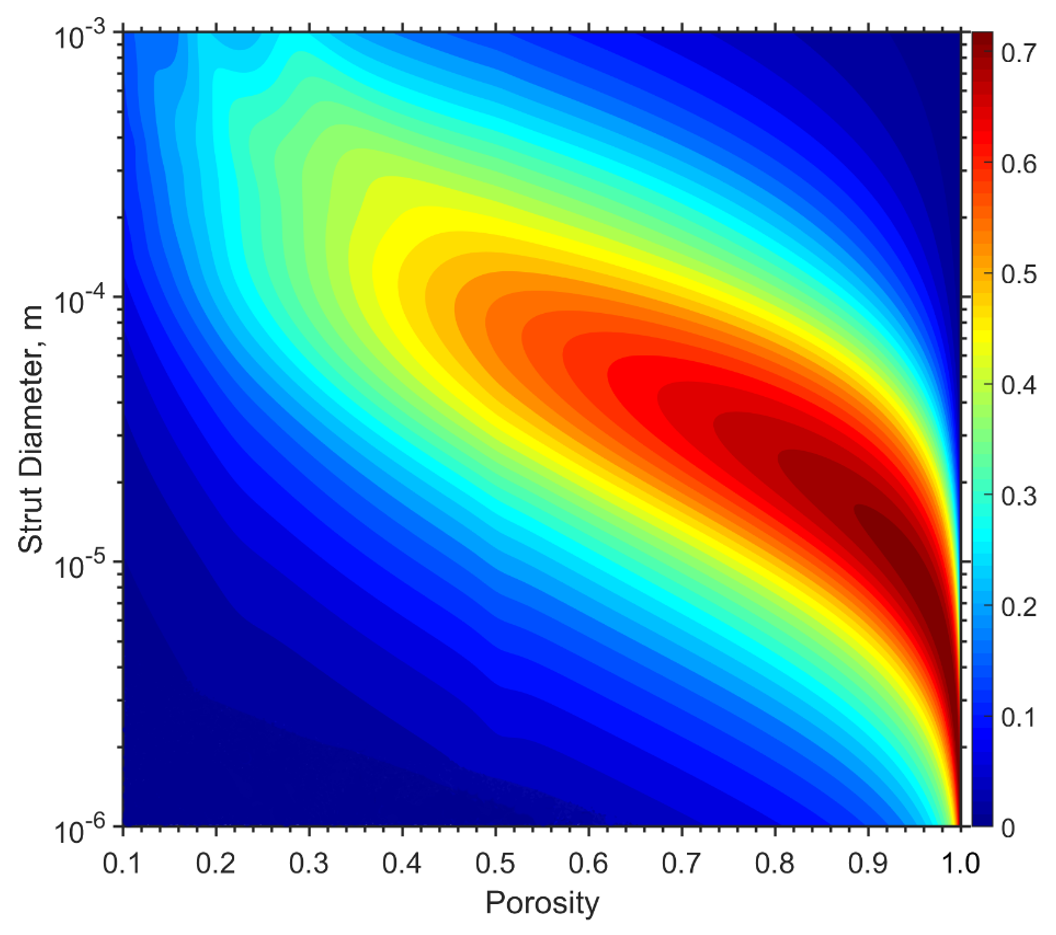
Figure 8: SAA for a 50 mm thickness microlattice structure, with each lattice cell having strut diameters ranging from 1 micrometer to 1 mm and cell porosities from 0.1 (very dense) to almost unity (very open).
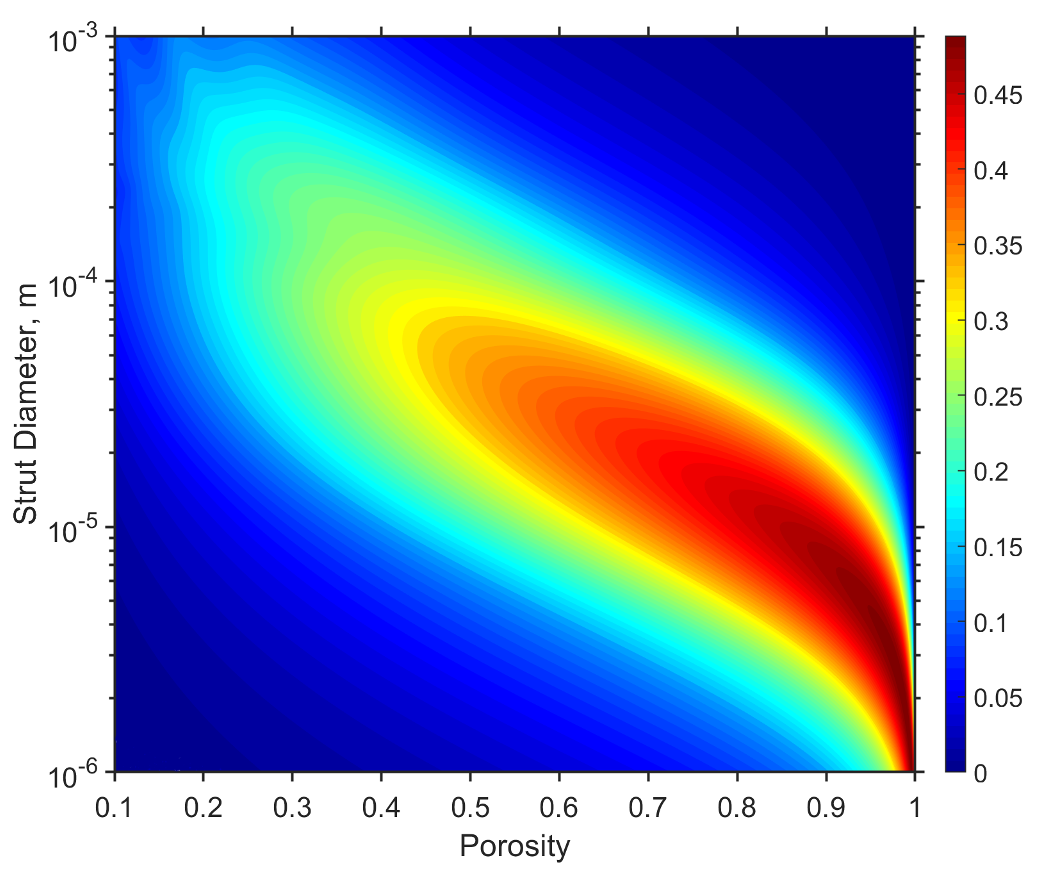
Figure 9: SAA for 20 mm thickness microlattice structure, with each lattice cell having strut diameters ranging from 1 micrometer to 1 mm and cell porosities from 0.1 (very dense) to almost unity (very open).
Designing for Perfect Sound Absorption
For a given thickness of porous material with corresponding quarter-wavelength frequency, a design proposal is to set the cell size to be approximately two times (2X) the viscous penetration depth of the fluid boundary layer (Ref. 3), l_{vor}=\sqrt{2\mu_f/(2\pi f\rho_f)}, where \mu_f is the dynamic fluid viscosity, \rho_f is the fluid density, and f is the frequency. If we have a lattice cell sample thickness of 50 mm in air at 20°C, for example, the quarter-wavelength frequency is 1715 Hz, which is the frequency at which maximum sound absorption would occur. To achieve maximum absorption at this frequency, we then choose the cell strut length to be 2 x lvor = 0.11 mm.
Near perfect absorption is then achieved at 1715 Hz. Systematically reducing the cell strut length to reduce the cell porosity will bring enhancements in low-frequency absorption, along with a sacrifice of some performance in the higher frequencies, as shown in Figure 10. This process of cell densification results in an increase of the dynamic viscous dissipation per unit cell volume. For a cell strut length of 1.2 x lvor, the SAA is estimated as 0.72, which is in the desirable range of the SAA contour map for 50 mm samples (Figure 8), and this cell design offers a very good balance of low- and higher-frequency absorption.
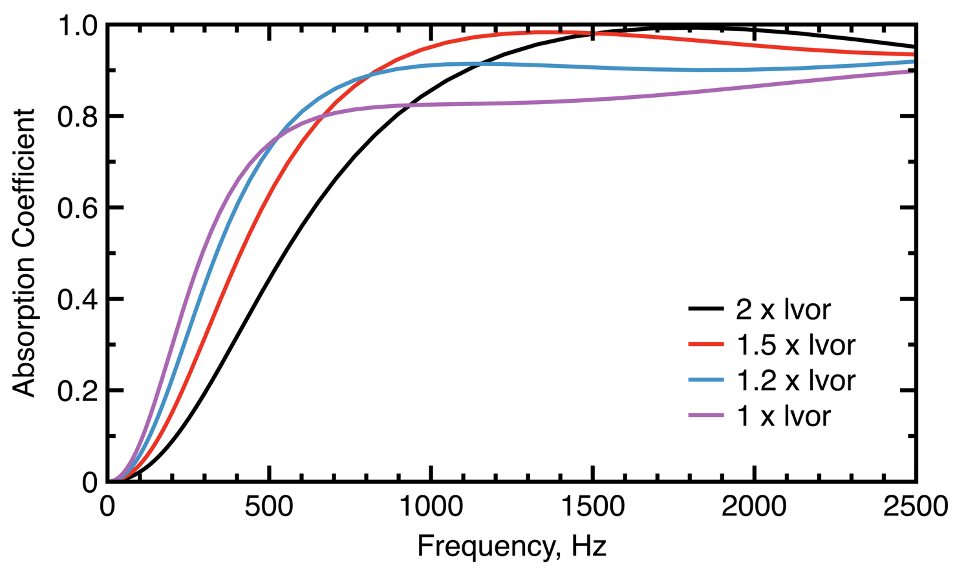
Figure 10: Unit lattice cell sound absorption for a 50 mm thickness sample, having a strut diameter of 5 micrometers, and a strut length based on multiples of lvor at the quarter-wavelength frequency of 1715 Hz.
Design for Broadband Sound Absorption
An even simpler approach is to choose a default target design frequency of 1000 Hz and set the cell strut length equivalent to the viscous boundary layer penetration depth of lvor = 0.07 mm. This will lead to a broadband sound absorption behavior, as shown in Figure 11, and a relatively high value of SAA = 0.71. It then becomes possible to further fine tune the sound absorption behavior by modifying the diameter of the cell struts (Figure 12), which will also increase the dynamic viscous dissipation per unit cell volume.
When available, it is most efficient to work directly with the SAA contour maps as they provide immediate guidance toward which lattice cell designs will provide effective broadband sound absorption performance.
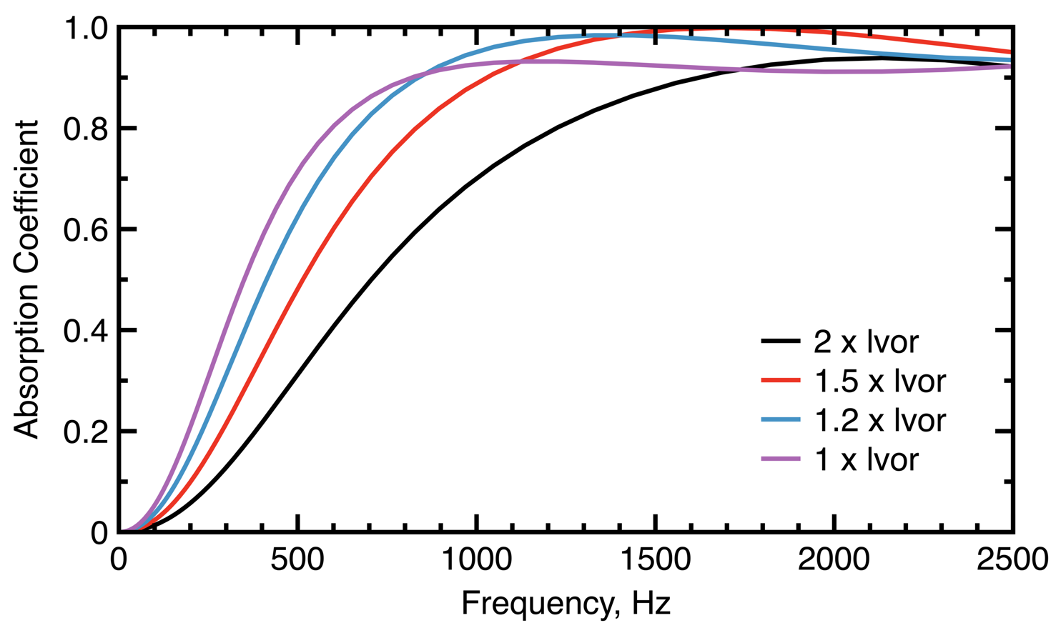
Figure 11: Unit lattice cell sound absorption for a 50 mm thickness sample, having a strut diameter of 5 micrometers and a strut length of lvor at a 1000 Hz target frequency.
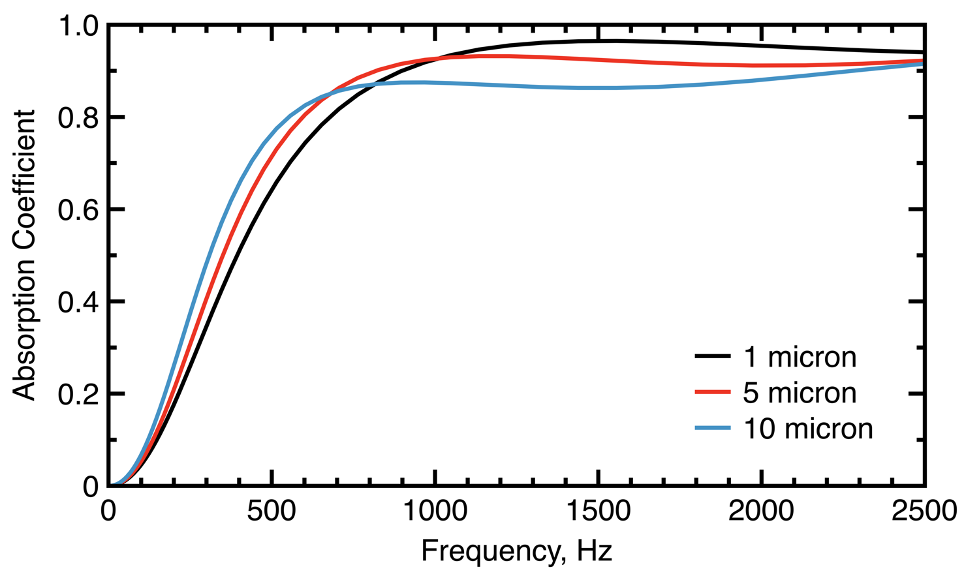
Figure 12: Unit lattice cell sound absorption for a 50 mm thickness sample, with varying strut diameters and a strut length of lvor at a 1000 Hz target frequency.
Summary
If the goal is to achieve near perfect absorption for a specific layer thickness, then choose 2X the viscous boundary layer penetration depth at the quarter-wavelength frequency as the cell strut length. For enhanced sound absorption at lower frequencies, i.e., a higher value of SAA, increase the viscous dissipation within the cell by either reducing the cell strut length or by reducing the diameter of the struts. Combined with optimally grading the porosity through the thickness of the microlattice layer (Ref. 4), and with controlling the anisotropy of the cells (Ref. 5), will allow even further improvements in tailored sound absorption performance.
Of course, this is all dependent upon the printing resolution limit of the additive manufacturing technology, but the potential benefits of the “design to print” approach described in this blog post are within grasp. With continuous improvements in additive manufacturing speed and resolution, I am confident that we will be able to realize the high-performance lattice cell designs presented here.
Example Application: Acoustic Encapsulation of an Electric Drive Motor
We have demonstrated how to optimize the design of the lattice structure to provide optimum sound absorption at specific frequencies or provide high levels of broadband sound absorption over a wide frequency range. It then is conceptually possible to imagine utilizing the strengths of additive manufacturing to develop porous components with localized regions of lattice cells having optimized absorption, tailored to counteract high levels of sound radiation from a vibrating component at specific frequencies, such as for the encapsulated electric motor shown in Figure 13. This solution would also help reduce material usage and cost, becoming an exciting target for the future use of additive manufacturing technologies in acoustics and NVH applications.
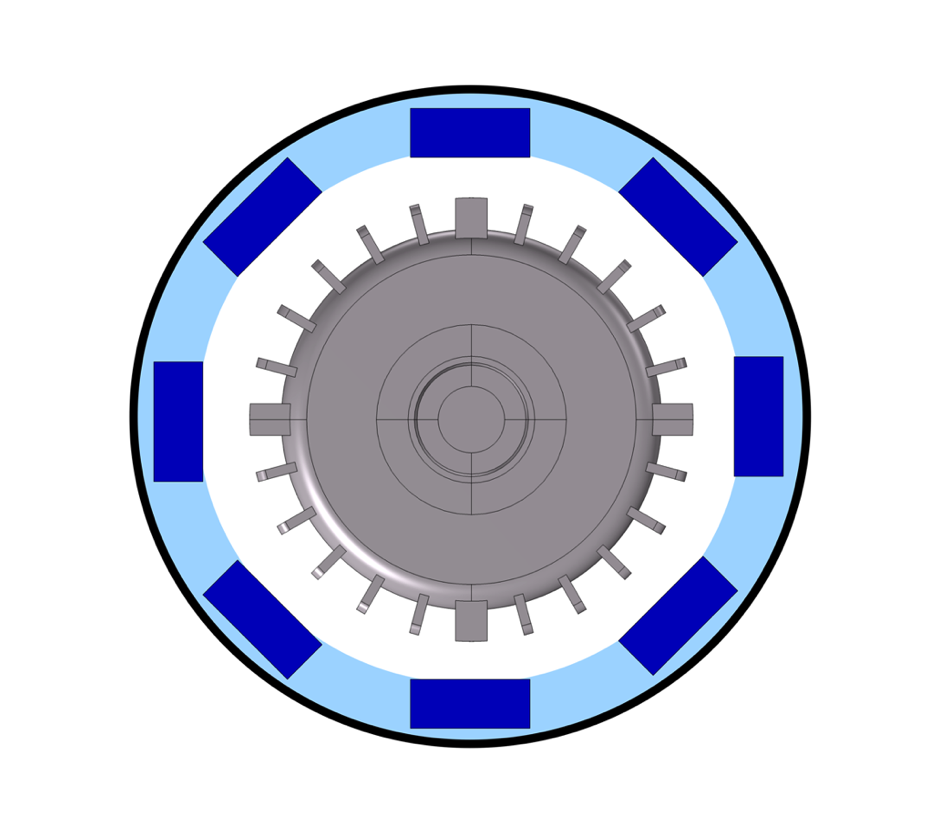
Figure 13: Electric motor with distributed acoustic encapsulation optimized according to engine noise radiation patterns.
References
- P. Semeniuk et al., “Dynamic equations of a transversely isotropic, highly porous, fibrous material including oscillatory heat transfer effects,” Journal of the Acoustical Society of America, no. 146(4), pp. 2540–2551, 2019.
- P. Semeniuk et al., “Acoustics modelling of open-cell foam materials from microstructure and constitutive properties,” Journal of the Acoustical Society of America, no. 149(3), pp. 2016–2026, 2021.
- Cai. et al., “Sound absorption by acoustic micro-lattice with optimized pore configuration,” Journal of the Acoustical Society of America, no. 144(2), pp. EL138–EL143, 2018.
- Boulvert et al., “Optimally graded porous material for broadband perfect absorption of sound,” Journal of Applied Physics, no. 126, 175101, 2019.
- Mao et al., “Twist, tilt and stretch: From isometric Kelvin cells to anisotropic cellular materials,” Materials and Design, no. 193, 108855, 2020.
About the Author
B.P. (Brad) Semeniuk is a consulting engineer based in Switzerland, with more than 30 years of experience in the development of numerical simulation methods for the acoustics of materials and the development of products for NVH applications. He currently works on the development of next-generation microstructure-based modeling approaches for porous materials and often publishes these efforts in collaboration with the Department of Technical Mechanics, KTH Royal Institute of Technology, Stockholm, Sweden. He may be contacted directly at semeniuk@kth.se or poreacoustics.com.





Comments (0)