An expansion fan occurs when a supersonic flow turns around a convex corner. When analyzing this phenomenon, you need to make sure your simulation results are accurate and agree well with existing theory. Here, we will show you that this is possible with the COMSOL Multiphysics® software and CFD Module. We discuss a benchmark model of a supersonic expansion fan and compare it to the inviscid compressible flow theory. We’ll also share a couple of tricks for improving this model.
Improving Supersonic Flight with Reliable Supersonic Flow Analysis
Supersonic flows, which are faster than the speed of sound and Mach 1, are not something we encounter on a daily basis. However, they are particularly relevant in fields like the aerospace industry. One example is NASA, who studies supersonic flight to advance aeronautics research and design vehicles that perform well at supersonic speeds. (A new supersonic passenger jet is a recent example.)

A supersonic jet. Image by EyeMindSoul. Licensed under CC BY 2.0, via Flickr Creative Commons.
Simulation can be a powerful tool for analyzing supersonic flow for these and other purposes. But when you obtain results, you want to be confident in their accuracy. COMSOL Multiphysics includes features and functionality that enable you to generate reliable results for trustworthy analyses. To demonstrate this, we’ll share a benchmark model of an expansion fan, a key element of a supersonic flow.
Expansion Fans: An Important Phenomenon in Supersonic Flows
Expansion waves occur when a supersonic flow encounters a convex corner, also called an expansion corner, and turns away from itself, increasing the area. (The opposite scenario of a supersonic flow turning into itself and causing a reduction in the area creates an oblique shock wave.)
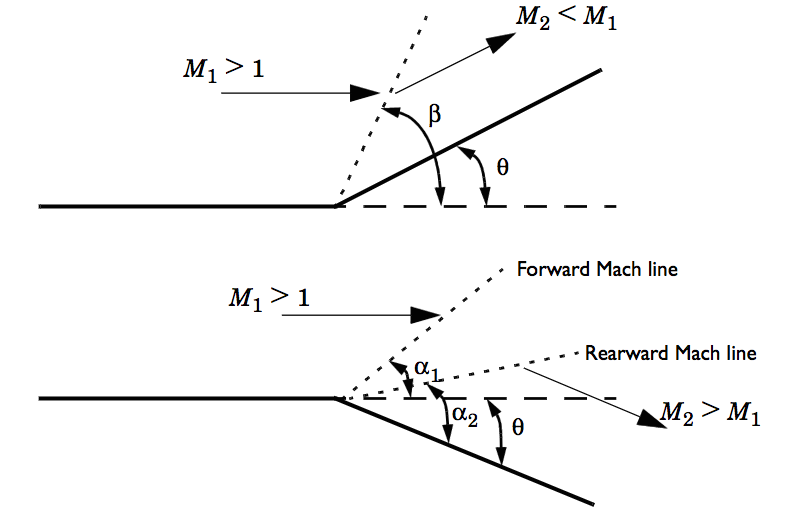
An oblique shock wave (top) and a Prandtl-Meyer expansion fan (bottom).
For supersonic expansion fans, otherwise known as Prandtl-Meyer expansion fans, the total conditions don’t change across the wave and entropy is conserved. Further, there is a decrease in static temperature, pressure, and density as well as an increase in the Mach number. Expansion fans are isentropic processes that generate continuous and smooth changes in the flow, causing the flow’s total properties to be conserved. Here, total values are the values that the flow properties produce if brought to stagnation, while static values represent the actual values of the flow properties at a certain speed.
How Accurate Is Our Expansion Fan Tutorial?
Our 2D example model investigates an expansion fan that has a 15° expansion corner, supersonic inlet flow with Mach number 2.5, and assumed supersonic flow at the outlet. For our analysis, we assume that the flow is inviscid and therefore apply a Slip boundary condition to the walls. The fluid in this model is air.
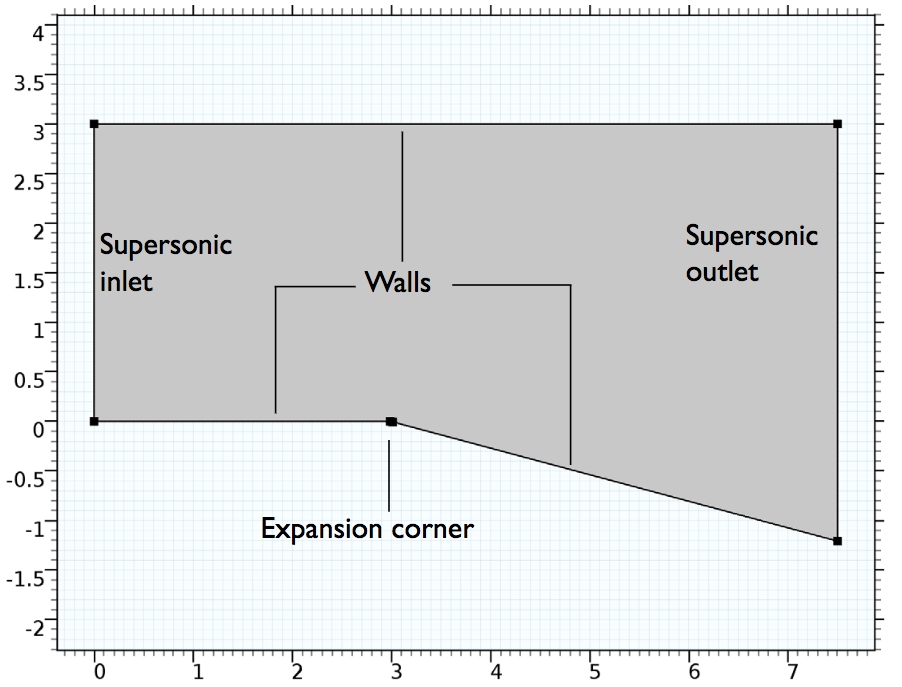
The expansion fan geometry.
To solve this problem, we use the inviscid compressible flow equations along with the High Mach Number Flow, Laminar interface in the CFD Module. To prove that the tutorial’s results are accurate, we can compare them to the inviscid compressible flow theory. Let’s jump ahead to these results now.
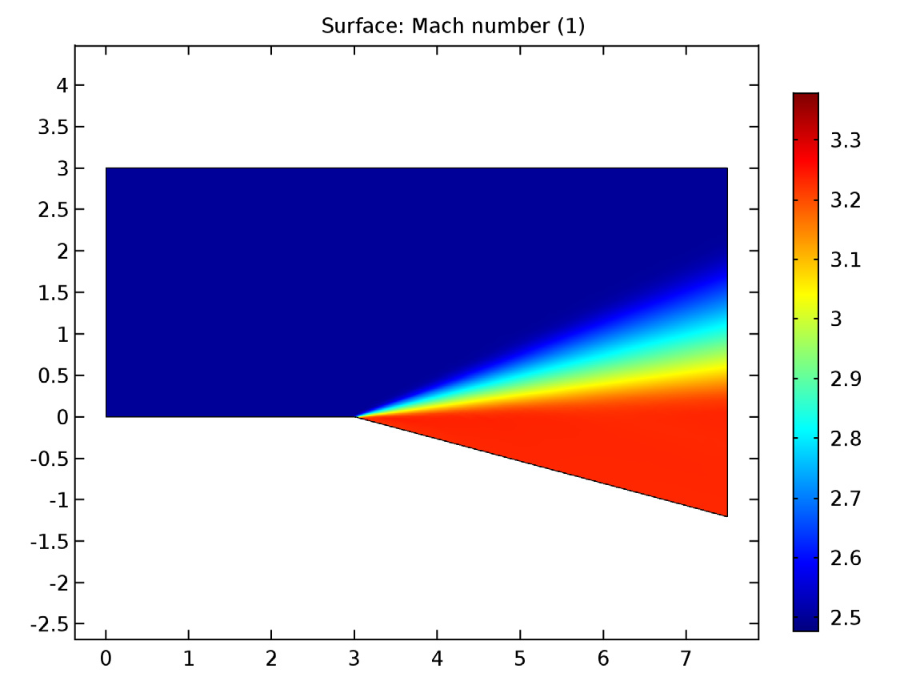
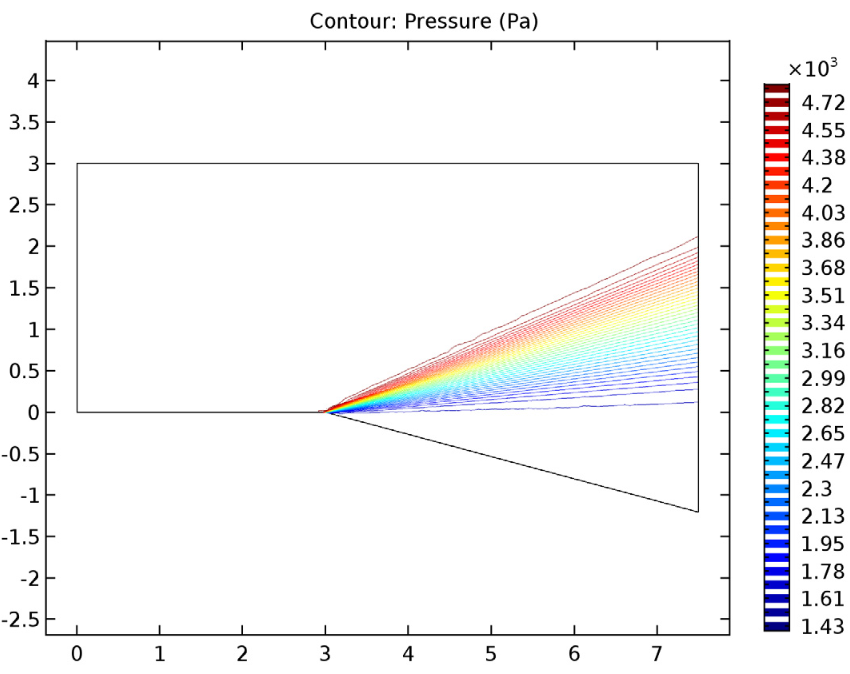
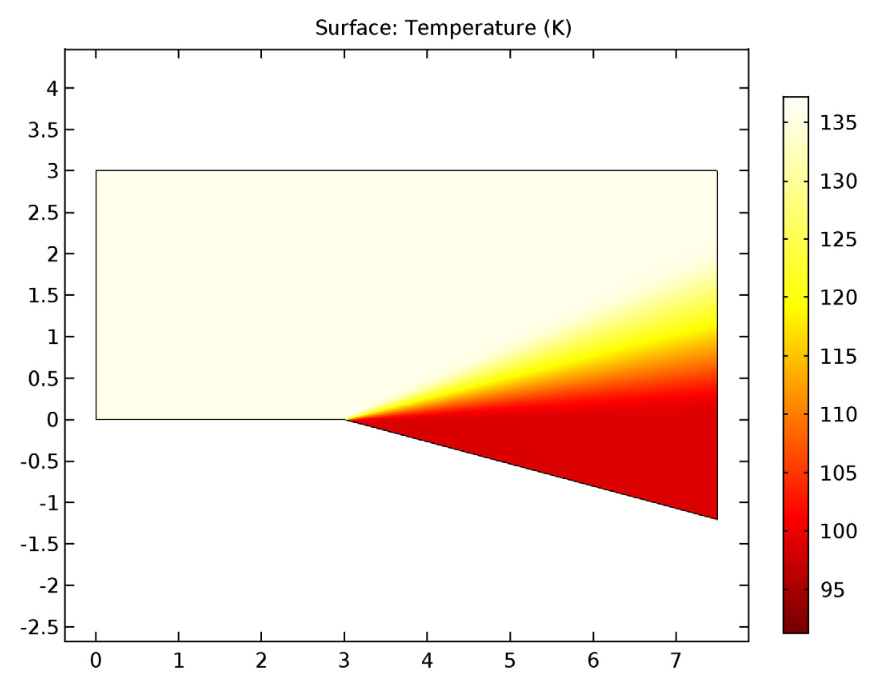
The expansion fan’s Mach number (left), pressure contours (middle), and temperature contours (right).
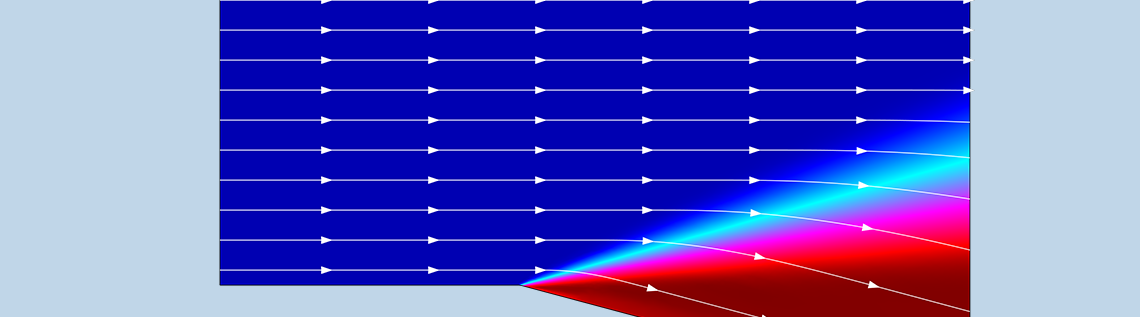
We see that the supersonic flow past the expansion corner expands in a succession of Mach or infinitesimal waves. These increase the Mach number while simultaneously decreasing the static pressure and temperature — as expected for expansion fans. As for the velocity streamlines, these smoothly vary their direction over the expansion fan, eventually becoming parallel to the surface below.
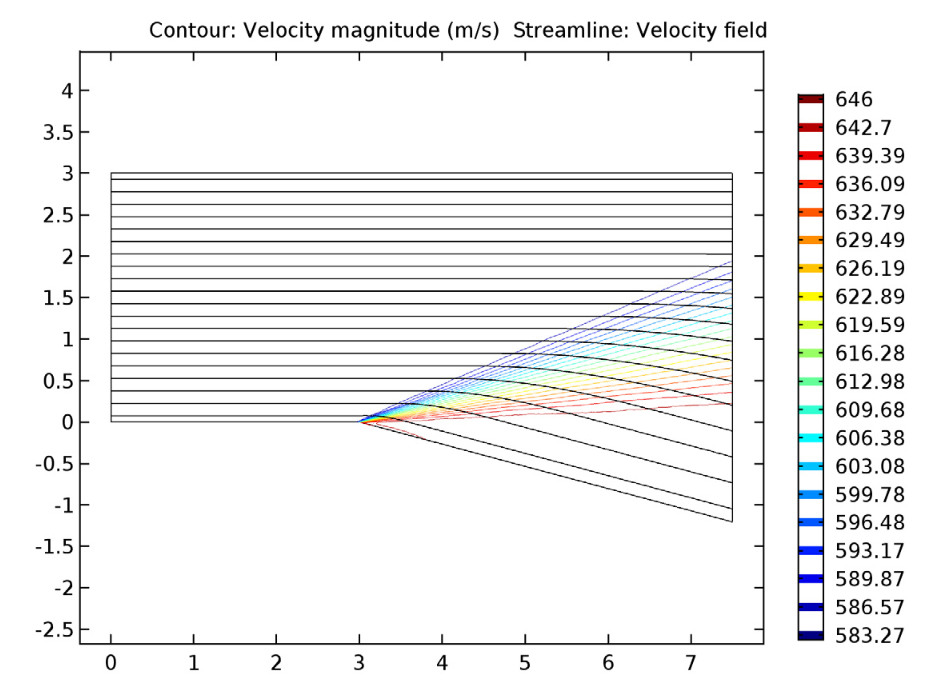
The expansion fan’s velocity contours and streamlines.
Moving on, let’s find out how the model’s results compare to those from the compressible flow theory. In the table below, we see that the Mach number from the simulation agrees well with the inviscid flow theory. We can also confirm that the total properties of the flow are conserved and similar to existing theory.
| Mach Number | Total Temperature | Total Pressure | Total Density | |
|---|---|---|---|---|
| Model | 3.2331 | 305.432 K | 82,213 Pa | 0.93787 kg/m3 |
| Compressible Flow Theory | 3.2372 | 305.432 K | 82,737 Pa | 0.94347 kg/m3 |
From this, we can conclude that our simulation results correlate well with those gathered from the inviscid compressible flow theory. As such, CFD models like our Expansion Fan tutorial can help to accurately analyze supersonic flow phenomena.
Click the button below to try modeling this benchmark example, which we improved using a few simple tricks:
- To avoid sharp gradients and discontinuities, we rounded the corner in the model
- To refine the mesh at the expansion fan, we used the Adaptive Mesh Refinement feature
Expand Your CFD Knowledge with These Tutorials and Blog Posts
- Find other CFD benchmark tutorials:
- Browse through our collection of CFD blog posts




Comments (0)