
What is the relation between the extremely popular band One Direction, quantum mechanics, and cosmology? Stephen Hawking may just have explained this relation in one of his recent talks at the Sydney Opera House. It has to do with the prediction of parallel universes, where we, in an infinite number of worlds, could find worlds that are almost identical to ours but with all possible permutations and differences, much like the 410-page books in The Library of Babel by Borges.
One Direction Goes in Two Directions
During a recent event, Stephen Hawking was asked by an interviewer about the cosmological implications of Zayn leaving One Direction, breaking the hearts of millions of girls. His answer was brilliant, empathetic, and gave an incredibly entertaining teaser to theoretical physics: “My advice to any heartbroken young girl is to pay close attention to the study of theoretical physics. Because one day there may well be proof of multiple universes. It would not be beyond the realms of possibility that somewhere outside of our own universe lies another different universe — and in that universe, Zayn is still in One Direction.”
Before we continue analyzing Hawking’s answer, though, let’s look into two of the exciting theories that predict parallel universes.
Quantum Worlds
In quantum mechanics, the solutions to the Schrödinger equation, the wave functions, result in probability functions for the position of elementary particles in time and space through linear combinations of wave functions. For example, electron density wave functions result in orbital probability functions for atoms and molecules.
Let us look at an example of the formulation of the Schrödinger equation for the hydrogen atom:

The time-dependent Schrödinger equation with the wave function denoted ψ (1). For definite energy states (2), we can re-write the equation in a time-harmonic form, thus giving (3). The potential energy, V, for the electron depends only on the radius and the wave function can be formulated in spherical polar coordinates (4). The wave functions for different energy levels, En, can be expressed as products of the spherical harmonics (Yl,m) and the amplitude (Fl), where l denotes the quantum number for the total angular momentum and m denotes the z-component of the angular momentum. Solving the Schrödinger equation (3) in spherical polar coordinates gives the wave function (4).

Wave functions for single electrons are called orbitals. Linear combinations (superposition) of wave functions are also solutions to the Schrödinger equation for the hydrogen atom. The orbitals with the quantum number l = 0 are always spherically symmetric. Orbitals with l = 1 are denoted p orbitals and show a clear angular dependency. Orbitals with l = 2 are called d orbitals, which show an even more complicated angular dependency. The plots show isosurfaces of a few wave functions.
In a similar way, physicists and physical chemists have been able to compute the table of elements with the possible stable elements in this Universe.
The measurement of a particle’s position and time is associated with an uncertainty that says that the more precisely the particle’s position is determined, the less precisely its momentum can be determined. This is known as the Heisenberg uncertainty principle after the scientist who formulated it. For example, if the position of a particle is known exactly, its momentum cannot be determined at the same time.
In quantum mechanics, wave function collapse occurs when the position or momentum is observed. This can also be explained by decoherence when a particle interacts with its environment. This means that when a particle is measured, the wave function no longer describes it (or appears to no longer describe it, according to decoherence) and the particle will be found in only one place.
However, the many-worlds interpretation of quantum mechanics, initially formulated by Everett, denies the collapse of the wave function. Instead, it derives many possible parallel universes, where all of the possible linear combinations (superpositions) of the wave function are expressed. The Universe would be composed of a quantum superposition of very many, possibly non-communicating, parallel universes or quantum worlds.
Eternal Inflation
The theory of inflation describes the beginning of the Big Bang as an extremely small inflating lump of substance, much smaller than an atom in volume. The little lump of substance doubled in mass, at constant density, in regular intervals of about 10-38 seconds. This took place around 260 times and created all of the mass in our Universe in about 10-35 seconds!
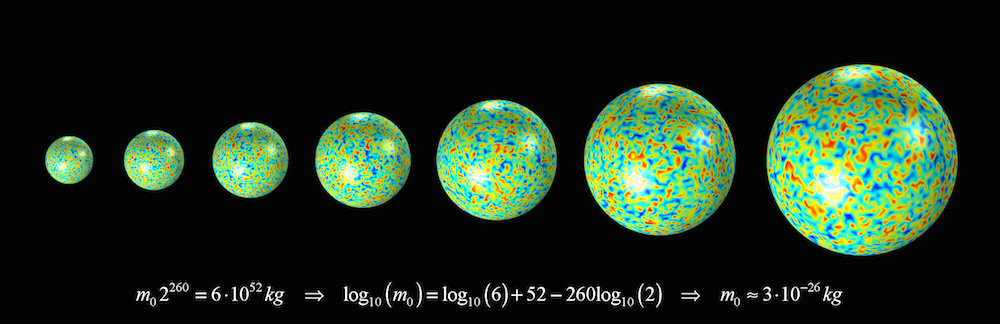
A little lump of substance doubling its mass and volume during inflation, getting its energy to create mass from antigravity, and with quantum fluctuations, due to Heisenberg’s uncertainty principle, providing the structure that later formed the cosmic structure of our Universe. The mass of this little lump was about 3·10-26 kg. Compare that to the mass of the hydrogen atom, which is about 1.7·10-27 kg!
The energy for creating this mass — remember E = mc2 — originated from the antigravity force that the inflating substance produced, which expended just enough energy to double the substance’s mass at constant density. Considering that the total mass of the Universe is estimated to 6·1052 kg, that is a lot of energy that gravity ended up owing. As a comparison, the Nagasaki bomb converted 1 g of mass to different types of energy. This would explain why gravity has negative energy, i.e., work is required to separate two objects attracted by gravity.
Eternal inflation also predicts that what we call the Universe is only one of an infinite number of Hubble volumes in an infinite universe — Hubble volumes created by eternal inflation. These Hubble volumes are similar to our Hubble volume but with different cosmic structures. During the early stage of inflation, quantum effects created the cosmic seed fluctuations responsible for our Hubble volume’s cosmic structure. Regions of space that now contain galaxies were smaller than an atom, where quantum effects were relevant. At this scale, the cosmic seed fluctuations can be explained by Heisenberg’s uncertainty principle, which prevents uniformity in any substance, including the inflating matter.

Some Hubble volumes in an infinite universe with an infinite number of Hubble volumes could be identical or almost identical to our Hubble volume that we call the Universe.
Most Hubble volumes have different distribution of matter compared to ours, but since there is an infinite number of them, there could also be an almost infinite number of variants of Hubble volumes that are of the same material distribution. There could also be an almost infinite number of variants of worlds that are identical or almost identical to our world.
Unifying Multiverses
The many-world interpretation of quantum mechanics leads to an almost infinite number of universes expressing an almost infinite number of what MIT cosmologist Max Tegmark calls Level III parallel universes. In a similar fashion, inflation theory may predict an infinite number of Hubble volumes, forming the Level I multiverse according to Tegmark, author of the book Our Mathematical Universe.
There could therefore be an almost infinite number of variants of Level I parallel universes with the same number of elementary particles as our Universe but arranged in a different way, since the wave function and quantum fluctuations would create an almost infinite number of combinations. In this sense, Tegmark speculates, the Level III and the almost identical Level I parallel universes could actually be one and the same, so that the wave function for a system describes its infinite copies throughout space.
Hawking on Zayn Leaving One Direction
The many-worlds interpretation of quantum mechanics and the theory of inflation have been fantastic subjects for imagination.
Recently, during an event at the Sydney Opera House where Stephen Hawking participated through a hologram, he was asked the following question by the interviewer: “What do you think is the cosmological effect of Zayn leaving One Direction and consequently breaking the hearts of millions of teenage girls across the world?”
Hawking’s answer can be interpreted as a reference to inflation theory and, through unification, also to quantum worlds: “My advice to any heartbroken young girl is to pay close attention to the study of theoretical physics. Because one day there may well be proof of multiple universes. It would not be beyond the realms of possibility that somewhere outside of our own universe lies another different universe — and in that universe, Zayn is still in One Direction.”
Hawking’s comment can be explained using the schematic below. In this World, Zayn leaves the band. In World 1, however, Zayn stays with the band and nobody would ever know that he left the band in this World. In World 2, Zayn not only stays in the band, he also marries one of the girls that in this World are heartbroken. Not only that, in each of the millions of other worlds, World n = 3 to World n = millions, Zayn marries each one of the heartbroken girls in this World.
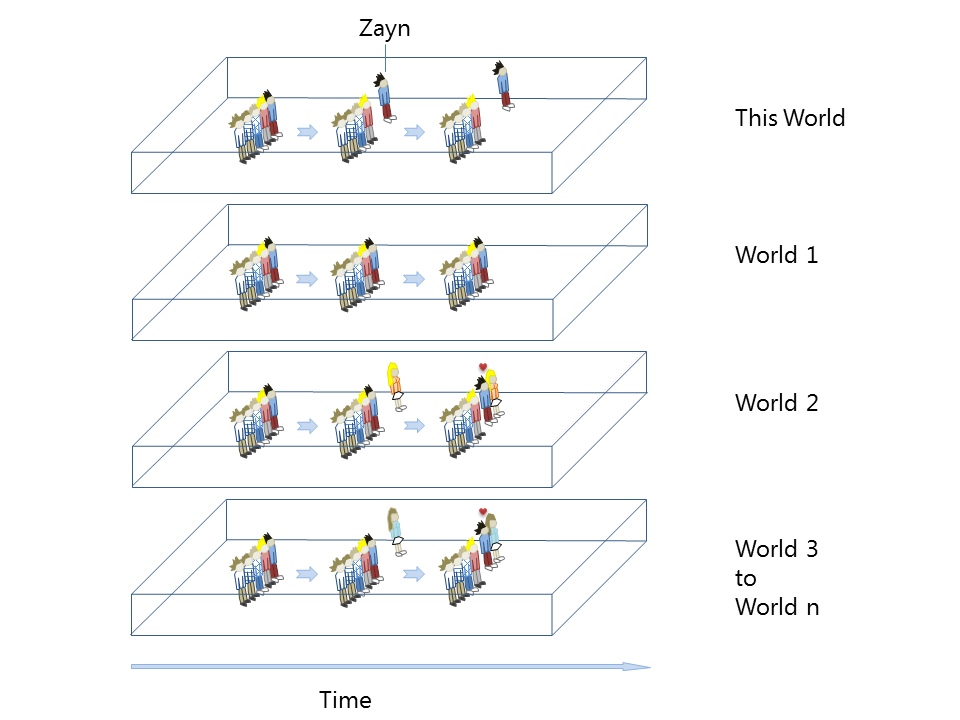
In millions of the almost infinite number of possible worlds, Zayn not only stays in the band, he also marries each of the heartbroken girls in this World.
Both the quantum worlds and the infinite number of Hubble volumes could be interpreted as a parallel world analogy to Jose Luis Borges’ The Library of Babel. The 410-page books in this library would be the analogy to all possible quantum worlds or Level I almost identical parallel universes, with identical Hubble volume and amount of material (410 pages), to what we call our Universe. All possible stories that you can ever imagine would eventually happen in any of these worlds!
Multiphysics Simulations
Meanwhile, and along the lines of Hawking’s advice, our advice to the heartbroken One Direction fans is to get an education in science and study the solution to the Schrödinger equation and the theory of inflation using instruments and equipment developed with the help of multiphysics simulations, see the figure below.
Luckily, the laws of physics are the same in the Level I and Level III multiverses, and the worldwide network license of the COMSOL Server software is valid in all Hubble volumes and in all Level III universes to run apps that simulate the Schrödinger equation.
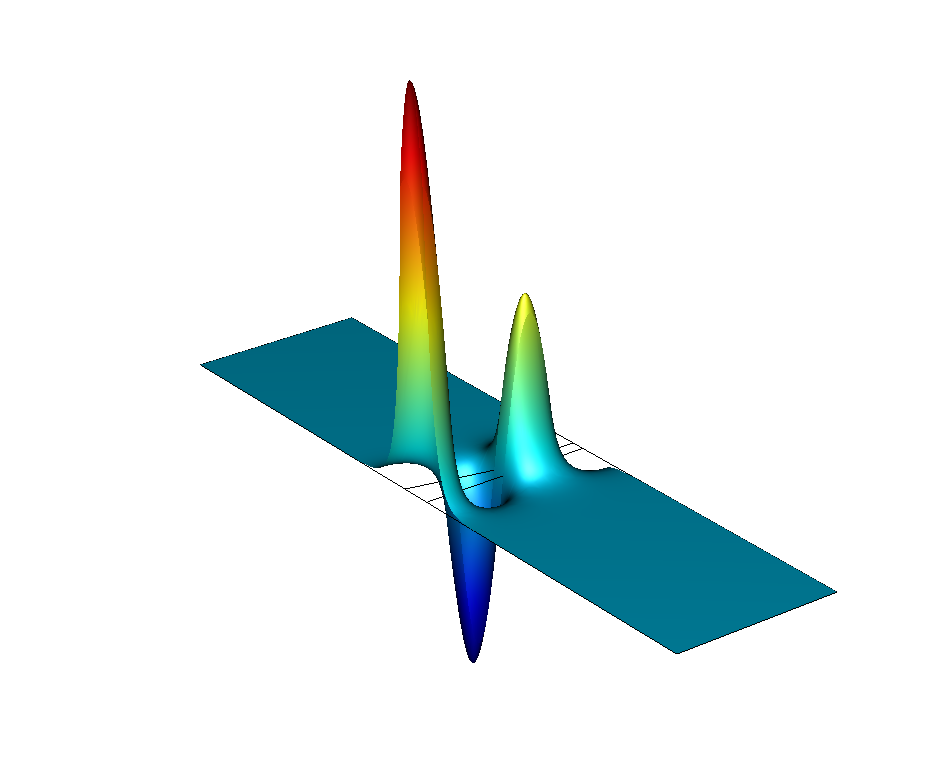
Simulation results showing the wave function for the electronic energy from a model of a conical InAs quantum dot. To compute the electronic states taken on by the quantum dot, the 1-band Schrödinger equation is solved.
Before deducing another parallel universe (or very many of them) where Zayn is still a member of One Direction, these girls may create exciting things such as quantum dots for quantum computers and biological labeling. They may also design and develop tools for deep-space exploration and for studying galaxies in this Hubble volume that we call our Universe.
In one of these worlds, a One Direction fan may be or become the founder and creator of the most powerful multiphysics software in the Universe! When and in which world, though?

In yet another world, Stephen Hawking is a priest in Cambridge marrying Zayn with a One Direction fan. In that world, people in Britain speak Chinese while English is spoken in China, but then of course called “Chinese”.
Read More about Multiphysics Simulations for Space Applications
- Simulation Helps Improve Atmosphere Revitalization Systems for Manned Spacecraft
- Metamaterials Make Physics Seem Like Magic
- Ed Ethridge of NASA, who used COMSOL Multiphysics in extracting water from the moon
- COMSOL for modeling the heat transfer of the Mars Rover, for protecting instrumentation
- Rosetta and Philae: A Historic Landing on a Comet
- William T. Vetterling: COMSOL Multiphysics and The Library of Babel (COMSOL Conference keynote video)






Comments (0)