To fillet or not to fillet, that is the question (that can bedevil the multiphysics analyst). When building finite element models, sharp edges can lead to local singularities and fields that are nonconvergent with mesh refinement. Rounding off these sharp edges by adding a fillet avoids this singularity. As it turns out, in many multiphysics models, these sharp edges and the resultant singularities do not necessarily negatively affect the results. Let’s find out more.
Electromagnetic Heating Around Sharp Corners
One of the most common problems solved with the COMSOL Multiphysics® software is that of electromagnetic heating, combining the solution to Maxwell’s equations, which solves for the current flow and resultant losses, and the solution to the heat transfer equation, which solves for the temperature distribution.
As mentioned in a previous blog post, when solving for the electromagnetic fields, sharp reentrant corners lead to locally nonconvergent electric fields and current density. Electromagnetic losses are the product of the electric field and current density, so the peak losses at a sharp corner will similarly go to infinity with mesh refinement.
However, the integral over the losses around the sharp corner will be convergent with respect to mesh refinement. This is one of the strengths of the finite element method, which solves the governing equation in the so-called “weak form”, which satisfies the governing partial differential equations in an integral sense: minimizing the total error in the model, but allowing (possibly infinite!) local errors.
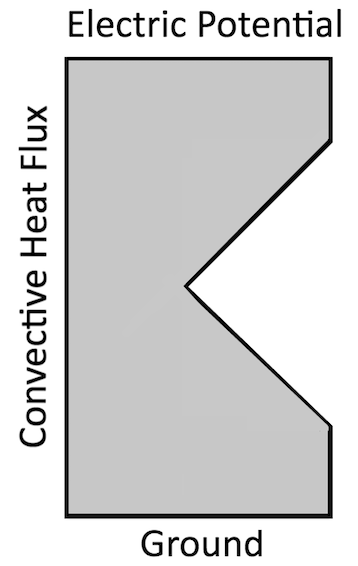
A schematic of a simple electromagnetic heating problem with a singularity at the inside sharp corner.
Let’s review this concept with a simple example, as shown in the image above. A rectangular domain with a sharp notch has an electric potential difference applied, leading to current flow and resistive losses in the material.
Below, we see a color plot of the resistive losses and the mesh used for different levels of mesh refinement at the sharp inside corner. At the highest level of mesh refinement, the losses appear very localized around the sharp corner.
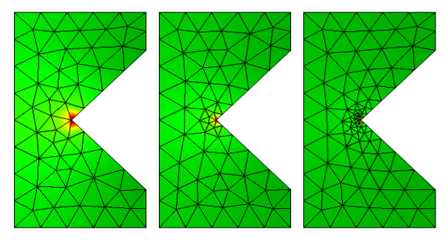
The electromagnetic losses on several different meshes.
At this sharp inside corner, the electric fields are actually theoretically infinitely large, since this geometry and the boundary conditions imply that the current must instantaneously change direction at a point. Also note that the sharp outside corners do not lead to singularities. As a consequence of the geometry and boundary conditions, the electric currents are not forced to change direction instantaneously at these points.
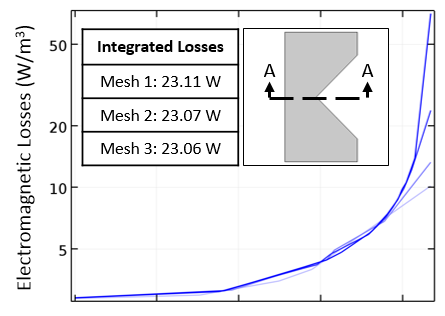
The resistive losses in log scale, plotted along a cut line, and a table of the integral of the losses for different meshes.
If we plot the losses at a cross-sectional line, as shown above, we can observe that the losses at the sharp point get larger and larger as the mesh is refined. However, the integral of the losses over the domain (roughly speaking, the area underneath the plotted curves) converges very quickly with mesh refinement.
Now let’s make this a multiphysics problem by additionally solving the heat transfer equation for the temperature distribution under steady-state conditions. These temperature fields are plotted below for several levels of mesh refinement, as well as the temperature at the sharp point.
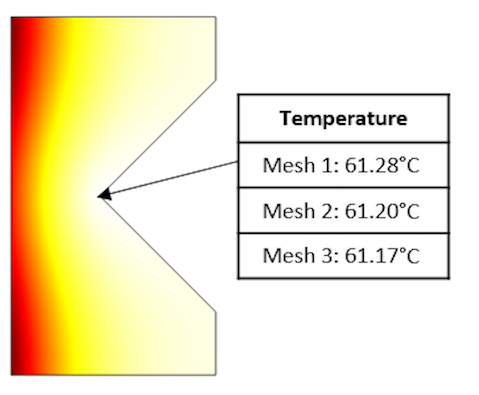
The temperature field and a table of the temperature evaluated at the sharp corner for different levels of mesh refinement.
We can see from these results that the temperature at the singular point — and, of course, everywhere else — is also very insensitive to the mesh refinement. This is for two reasons. First, as we just saw, the total resistive losses are quite insensitive to the mesh. Second, the diffusive nature of the steady-state heat transfer governing equation will return very similar temperature solutions as long as the total heat loads are similar. The transient temperature solution, on the other hand, can predict very high local temperatures if the heat load is very high, but this is also a local and relative effect, albeit in time. That is, spikes in the heat load distribution in space will be smoothed out over time, and in the limit of very long simulation times, the transient solution will approach the steady state solution.
Closing Remarks
What can we conclude from all of this information? If you are solving an electromagnetic heating problem and are only interested in computing the total electromagnetic losses and temperature distribution, you can usually avoid adding fillets to your model.
The advantages here are twofold. You do not need to go through the CAD modeling effort of adding any fillets to your geometry and you do not need an overly refined mesh in the sharp corners, which can save you the most valuable resource: time!





Comments (3)
Ivar KJELBERG
December 1, 2017Hi Walter,
thanks for an interesting blog, I would point out that depending on the physics these singularities have quite different effects, here obviously the fillet is not really required
I like to fillet off systematically i.e. for EM physics: all parts I use for force calculations (when possible), and in structural: all corners of high stress are worth to fillet off to avoid that the corner masks a true stress concentration location.
For the EM force calculation case the reason comes from the precision of the estimate of the derivatives of the Dependent variables and how these are handled at boundary discontinuous “sharp” corners. But similar integration on derivatives appear in other physics too, and one might then apply the fillet rule by similarity.
The nice thing with COMSOL is that all physics are treated in the same way, with the same methodology, so there are many effects one can analyse or act on by similarity, between the physics.
Sincerely
Ivar
abderrahmane aissa
December 30, 2017Hi sir,
thanks for an interesting blog.
please i need a tutoral of this blog
Cynthy Lee
May 31, 2018Great post! It’s an interesting angle to analyse electromagnetic heating, and maybe this machine can help you in your testing procedure:
testextextile.com/product/sharp-edge-tester-tt811/