
The COMSOL Multiphysics® software includes many built-in physics equations and interfaces, but there may be times when you need to implement physics that aren’t part of the software to solve your modeling problem. You can use the flexibility of the COMSOL® software to add user-defined equations via equation-based modeling. Today, we discuss using equation-based modeling to solve a shallow water equation, which can be used to analyze coastal erosion.
Analyzing Coastal Erosion with Shallow Water Equations
On the shoreline, crashing waves and the continuous movement of the tides cause coastal erosion, a phenomenon that removes sediment from beaches and wears away land.

A rock formation affected by coastal erosion. Image by John Nuttall — Own work. Licensed under CC BY 2.0, via Flickr Creative Commons.
Although coastal erosion has benefits, such as creating sand for beaches, it also causes damage to seaside property and habitats. To help predict this damage, researchers can use shallow water equations to learn more about coastal erosion. These equations enable scientists to model oceanographic and atmospheric fluid flow, thereby predicting what areas will be affected by coastal erosion and other issues, such as polar ice cap melting and pollution.
Shallow water equations are beneficial compared to the Navier-Stokes equations, which may be problematic depending on how free surfaces are resolved and the scale of the modeling domain. Today, we highlight a tutorial that showcases how to solve shallow water equations using the power of equation-based modeling.
Solving Shallow Water Equations in COMSOL Multiphysics®
In this shallow water equation model, we can describe the physics by adding our own equations — a feature called equation-based modeling. We use the General Form PDE interface and two dependent variables to ensure that the modeling process is straightforward. This way, we can easily define expressions as model variables, which comes in handy when defining the initial wave profile.
This simple 1D model uses the Saint-Venant shallow water equations to study a wave settling over a variable bed as a function of time.
The 1D model featured here would require substantial work to convert into a 2D model for solving typical applications. This tutorial is therefore most useful as an example of the benefits of equation-based modeling.
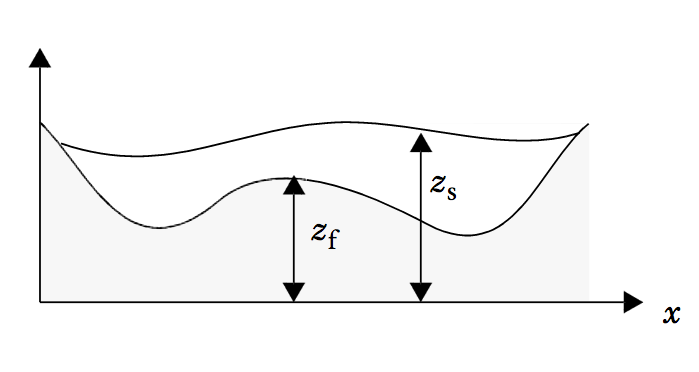
A vertical section of the fluid domain. Here, zf is the analytical expression for the seabed profile and zs is the water surface profile.
The model, which investigates shallow water in a channel, has constraints at both ends and uses a wave profile as the initial condition. In order to easily alter parameters like the wave amplitude and bed shape, we can use mathematical relations to represent the initial wave and bed shapes. Please note that the model has a difference in scale between the x– and y-directions, as seen in the plots below.
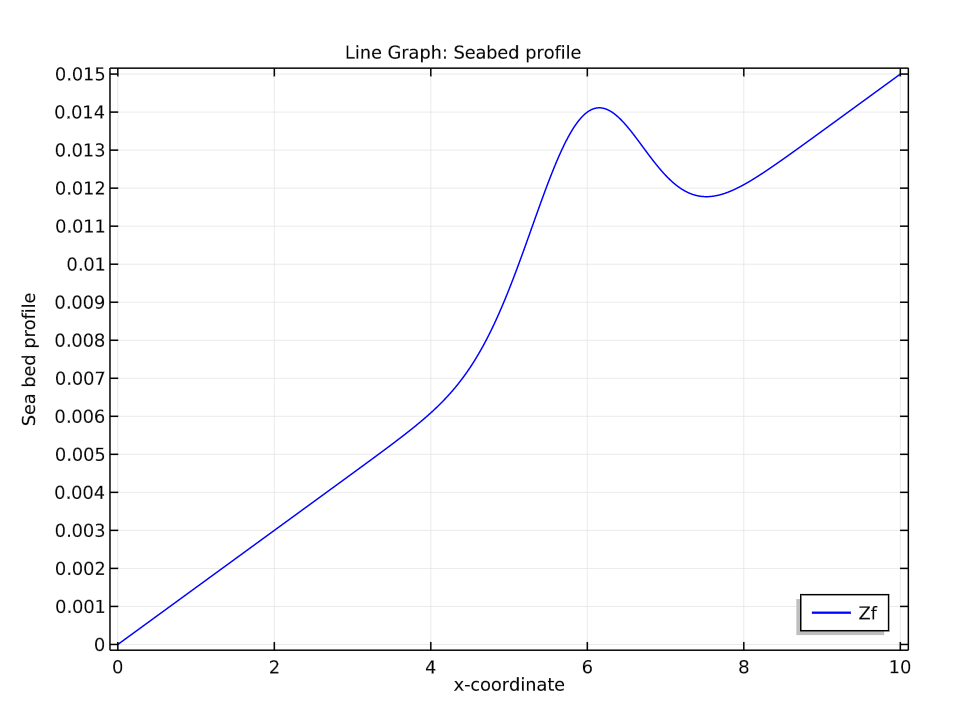
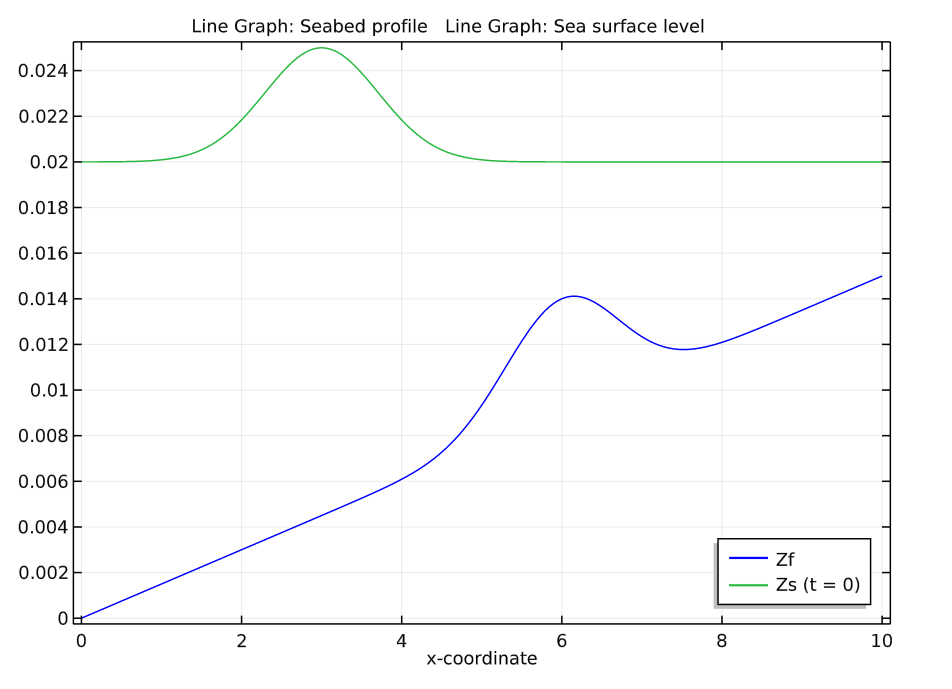
Plots of the seabed profile (left) and a comparison of the initial water surface profile with the seabed profile (right).
We see that the flow develops hydraulic jump discontinuities over time, which can cause instability in the solution. To stabilize the solution, we can add an artificial viscosity that makes the cell Reynolds number of order unity. The hydraulic jumps are replaced with steep fronts that can be resolved on a grid.
Switching gears, let’s take a look at our results. After running the simulation for 60 seconds, we see results that show the water surface and seabed slope at 6 different times, from the start of the simulation to 15 seconds later.
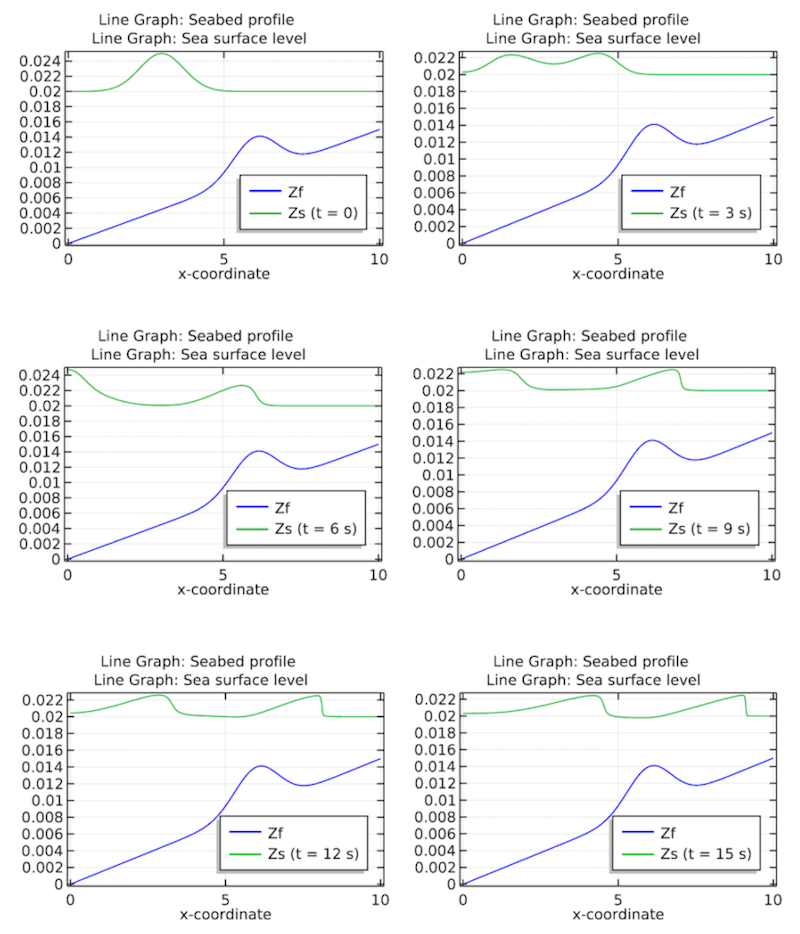
Plots of the seabed profile and water surface level at 3-second increments.
These results clearly indicate that the seabed topography influences the water surface elevation. This, in turn, affects the impact of coastal erosion.
We can share these custom results with others by creating and exporting an animation to help visualize our findings — something that is easy to do in COMSOL Multiphysics.
An animation of the simulation results.
As a next step, try this tutorial yourself by clicking on the button below.





Comments (0)