
In a recent blog post, we discussed how to use the Domain Decomposition solver for computing large problems in the COMSOL Multiphysics® software and parallelizing computations on clusters. We show how to save memory by a spatial decomposition of the degrees of freedom on clusters and single-node computers with the Recompute and clear option. To further illustrate the Domain Decomposition solver and highlight reduced memory usage, let’s look at a thermoviscous acoustics problem: simulating the transfer impedance of a perforate.
A Thermoviscous Acoustics Example: Transfer Impedance of a Perforate
If you work with computationally large problems, the Domain Decomposition solver can increase efficiency by dividing the problem’s spatial domain into subdomains and computing the subdomain solutions concurrently and sequentially on the fly. We have already learned about using the Domain Decomposition solver as a preconditioner for an iterative solver and discussed the possibilities to enable simulations that are constrained by the available memory. Today, we will take a detailed look at how to use this functionality with a thermoviscous acoustics example.
Let’s start with the Transfer Impedance of a Perforate tutorial model, which can be found in the Application Library of the Acoustics Module. This example model uses the Thermoviscous Acoustics, Frequency Domain interface to model a perforate, a plate with a distribution of small perforations or holes.

A simulation of transfer impedance in a perforate.
For this complex simulation, we are interested in the velocity, temperature, and total acoustic pressure in the transfer impedance of the perforate model. Let’s see how we can use the Domain Decomposition solver to compute these quantities in situations where the required resolution exceeds the margins of available memory.
Applying the Settings for the Domain Decomposition Solver in COMSOL Multiphysics®
Let’s take a closer look at how we can set up a Domain Decomposition solver for the perforate model. The original model uses a fully coupled solver combined with a GMRES iterative solver. As a preconditioner, two hybrid direct preconditioners are used; i.e., the preconditioners separate the temperature from the velocity and pressure. By default, the hybrid direct preconditioners are used with PARDISO.
As the mesh resolution becomes refined, the amount of memory used continues to grow. An important parameter in the model is the minimum thickness of the viscous boundary layer (dvisc), which has a typical size of 50 μm. The perforates are a few millimeters in size. The minimum element size of the mesh element is taken to be dvisc/2. To refine the solution, we divide dvisc by the refinement factors r = 1, 2, 3, 5. We can insert the domain decomposition preconditioner by right-clicking on the Iterative node and selecting Domain Decomposition. Below the Domain Decomposition node, we find the Coarse Solver and Domain Solver nodes.
To accelerate the convergence, we need to use the coarse solver. Since we do not want to use an additional coarse mesh, we set Coarse Level > Use coarse level to Algebraic in order to use an algebraic coarse grid correction. On the Domain Solver node, we add two Direct Preconditioners and enable the hybrid settings like they were used in the original model. For the coarse solver, we take the direct solver PARDISO. If we use a Geometric coarse mesh grid correction instead, we can also apply a hybrid direct coarse solver.
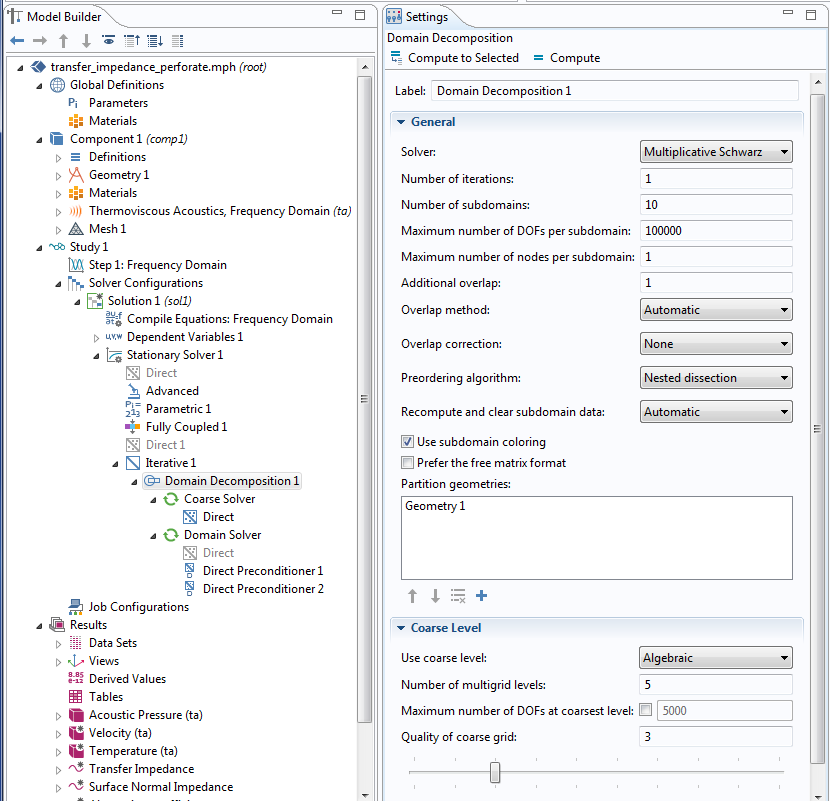
Settings for the Domain Decomposition solver.
Comparing the Resource Consumption for Three Solvers
We can compare the default iterative solver with hybrid direct preconditioning to both the direct solver and the iterative solver with domain decomposition preconditioning on a single workstation. For the unrefined mesh with a mesh refinement factor of r = 1, we use approximately 158,682 degrees of freedom. All 3 solvers use around 5-6 GB of memory to find the solution for a single frequency. For r = 2 with 407,508 degrees of freedom and r = 3 with 812,238 degrees of freedom, the direct solver uses a little bit more memory than the 2 iterative solvers (12-14 GB for r = 2 and 24-29 GB for r = 3). For r = 5 and 2,109,250 degrees of freedom, the direct solver uses 96 GB and the iterative solvers use around 80 GB on a sequential machine.
As we will learn in the subsequent discussion, the Recompute and clear option for the Domain Decomposition solver gives a significant advantage with respect to the total memory usage.
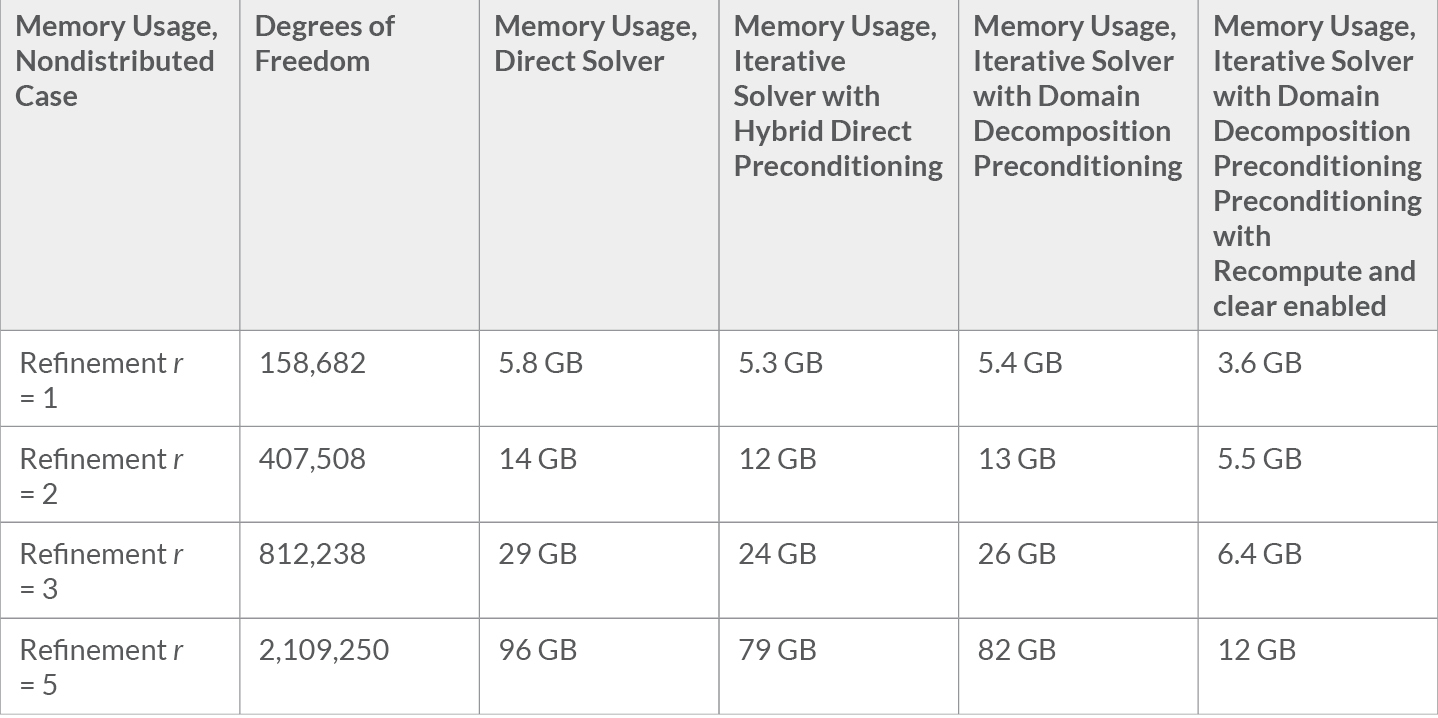
Memory usage for the direct solver and the two iterative solvers in the nondistributed case.
On a cluster, the memory load per node can be much lower than on a single-node computer. Let us consider the model with a refinement factor of r = 5. The direct solver scales nicely with respect to memory, using 65 GB and 35 GB per node on 2 and 4 nodes, respectively. On a cluster with 4 nodes, the iterative solver with domain decomposition preconditioning with 4 subdomains only uses around 24 GB per node.
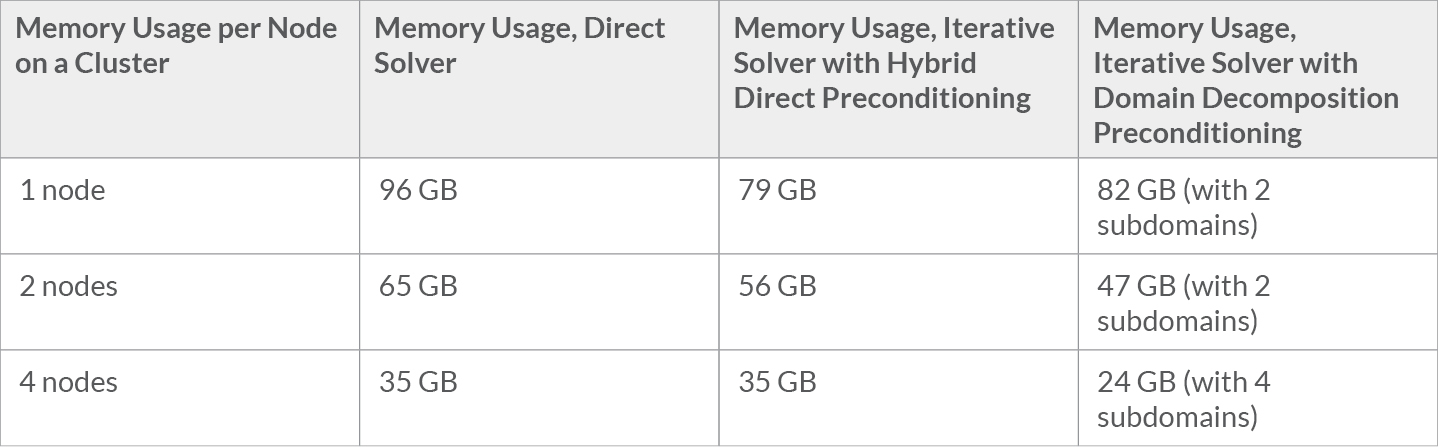
Memory usage per node on a cluster for the direct solver and the two iterative solvers for refinement factor r = 5.
On a single-node computer, the Recompute and clear option for the Domain Decomposition solver gives us the benefit we expect: reduced memory usage. However, it comes with the additional cost of decreased performance. For r = 5, the memory usage is around 41 GB for 2 subdomains, 25 GB for 4 subdomains, and 12 GB for 22 subdomains (the default settings result in 22 subdomains). For r = 3, we use around 15 GB of memory for 2 subdomains, 10 GB for 4 subdomains, and 6 GB for 8 subdomains (default settings).
Even on a single-node computer, the Recompute and clear option for the domain decomposition method gives a significantly lower memory consumption than the direct solver: 12 GB instead of 96 GB for refinement factor r = 5 and 6 GB instead of 30 GB for refinement factor r = 3. Despite the performance penalty, the Domain Decomposition solver with the Recompute and Clear option is a viable alternative to the out-of-core option for the direct solvers when there is insufficient memory.

Memory usage on a single-node computer with a direct solver for refinement factors r = 3 and r = 5.
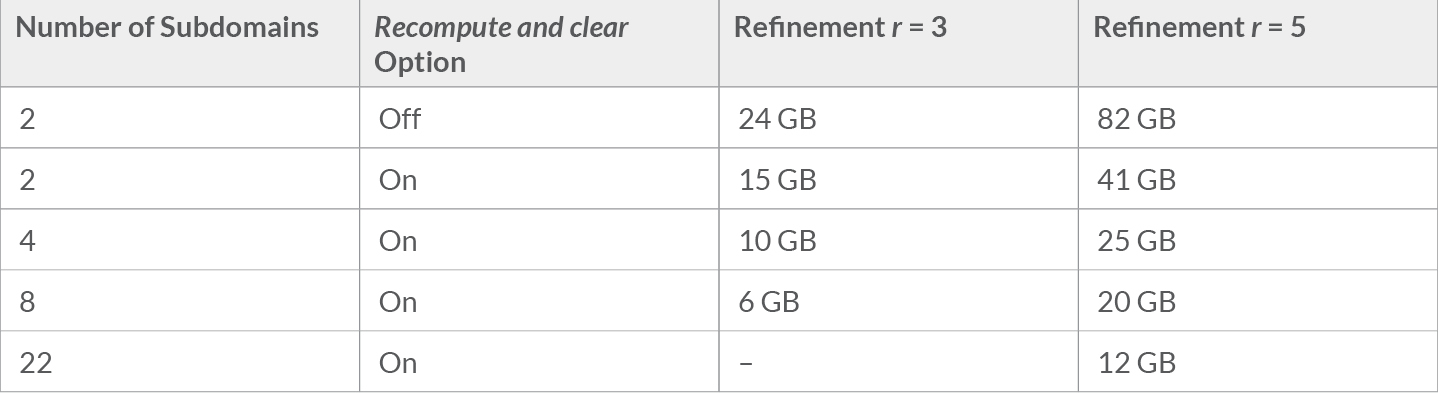
Memory usage on a single-node computer with an iterative solver, domain decomposition preconditioning, and the Recompute and clear option enabled for refinement factors r = 3 and r = 5.
As demonstrated with this thermoviscous acoustics example, using the Domain Decomposition solver can greatly lower the memory footprint of your simulation. By this means, domain decomposition methods can enable the solution of large and complex problems. In addition, parallelism based on distributed subdomain processing is an important building block for improving computational efficiency when solving large problems.
Further Resources
- In case you missed it, read Part 1 of this blog series: “Using the Domain Decomposition Solver in COMSOL Multiphysics®“
- Learn more about calculating the acoustic transfer impedance of a perforate on the COMSOL Blog





Comments (4)
James D Freels
November 25, 2016This is great information, but still a little bit difficult to follow the details. Do you have this model in the application library, or can you provide it here to reference ? Thanks.
Jan-Philipp Weiss
November 28, 2016Hi James, thank you for your feedback. Please follow the link to the tutorial model given in the blog post and choose Download the application files. You’ll find a version of the model with settings for the domain decomposition method. Best regards, Jan
Ivar Kjelberg
November 30, 2016Great news, you are coming gently to the process of integrating what others call “super-elements”.
I hope you manage to make it more streamlined, particularly for the decomposition of structural models: a full satellite is modeled as a hole, but by adding in many smaller components reduced to their essentials by a second, partially manual step: “model reduction”.
Now, you have all components in COMSOL too, it’s just that setting it all up, into a easily VV&C model structure, is still quite tedious.
But I’m confident you will master this challenge too, not only for structural, but PLS start simple, one physics at the time, do not have us wait until you have solved them all 😉
Farzad Kheradjoo
October 21, 2017This is wonderful!Thank you James for your explanations.
Im wondering what whould happen if we increase the number of subdomains while we keep the maximum number of DOFs per submdomain at 100000!How whould this affect our simulation?!
Many thanks in advance for your attention
Farzad