Adaptive Mesh Refinement: Quantitative Computation of a Rising Bubble Using COMSOL Multiphysics®
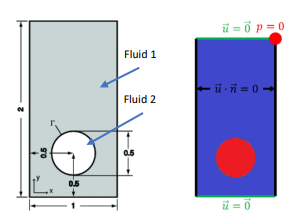
The mesh is a key component in numerical simulations as it represents the spatial discretization of the model geometry. To accurately measure the variation of the unknowns, a relevant mesh should have a high density of degrees of freedom in regions where the norm of the gradient of the quantity of interest is significant. Fine meshes, on the other hand tend to induce long computational times, especially when complex 3D physics (fluid mechanics, electromagnetism …) are involved. Another sensitive point regarding meshes is the fact that regions with high gradients are likely to move during time dependent studies hence it can be difficult to define a fixed mesh remaining relevant with time. The Adaptive Mesh Refinement (AMR) method implemented in COMSOL Multiphysics® can help to mitigate computational time while maintaining precision. Instead of using a fixed mesh throughout the simulation, the initial mesh is adapted to the solution while the simulation is computed. This adaptation is done by estimating an error indicator on the initial coarse mesh to identify high gradients areas, where the mesh will be refined. In this paper, rising bubbles models from literature, in both 2D and 3D are simulated. The AMR method is particularly relevant for the modelling of a two-phase flow since a fine mesh is needed around the interface, which evolves with time. In both 2D and 3D cases, the computational time is significantly reduced, by a factor of 5 in the 2D case while the precision is kept constant. The gain in both computational time and accuracy is quantified through a comparison between the results from the literature and those using the AMR technique. The efficiency of the AMR method is demonstrated here on the rise of a bubble to keep the physics involved simple enough. However, as the technique is particularly well suited for modelling problems involving high gradients in the field of interest, moving meshes and deformed geometry, it can be used on complex industrial cases such as numerical simulations of welding or additive manufacturing.
Download
- preney_presentation.pdf - 2.91MB
- preney_poster.pdf - 0.52MB
- preney_paper.pdf - 1.12MB
- preney_abstract.pdf - 0.03MB
