Studies & Solvers Blog Posts

The Power of the Batch Sweep
Have you ever run a large parametric sweep on your workstation overnight, only to discover the next morning that the parametric solver is still not finished? Enter the batch sweep.

How to Compute the Projected Area of a CAD File in COMSOL®
Learn about three approaches to computing the projected area of a CAD file and when to use each one.
How to Run COMSOL Multiphysics® from the Command Line
Did you know that you can run repeated variations of the same COMSOL Multiphysics® model file from the command line — and automatically export data?
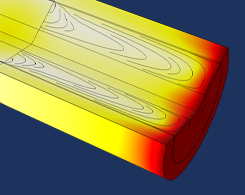
Strategies to Counter Small Automatic Time Steps
When solving a model, you may encounter a varying time step and discretization order, or NLfail or Tfail could be greater than 0. Use these strategies to improve the efficiency of the simulation.
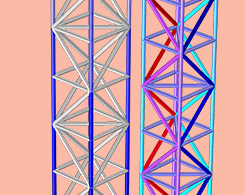
How to Perform a Sensitivity Analysis in COMSOL Multiphysics®
How do the parameters of your design affect its performance? Understanding this relationship is a valuable part of the design process. By performing a sensitivity analysis, you can do just that.
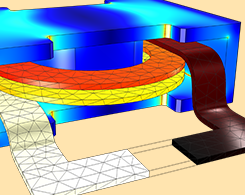
Which Study Type Should I Use for My Electrothermal Analysis?
What’s the best interface to use when implementing electrothermal analyses in COMSOL Multiphysics? We go over the interfaces, study types, and multiphysics couplings for high and low frequencies.
How to Use Solver Suggestions in Acoustics Modeling
When you model large, industry-scale acoustics, ever find it challenging to efficiently solve the problem with the hardware at hand? Enter the solver suggestions in COMSOL Multiphysics®.
Automatic Time Step and Order Selection in Time-Dependent Problems
Here’s an intro to the time-dependent solver log in COMSOL Multiphysics® and an in-depth look at the theory behind discrete time-stepping schemes and optimal time steps and discretization orders.
