
Creating the geometry for your model is one of the first steps of setting up a simulation. In the COMSOL Multiphysics® software, there are many geometry operations, tools, and functionality that enable you to do this. These include geometric primitives; Boolean, partition, and transformation operations; work plane operations; and other CAD tools. Here, we highlight all of this functionality and, near the end, link to a video tutorial series that shows how to use them while building your model geometry.
Geometry Creation in COMSOL Multiphysics®
There are four main ways you can generate the geometry for your simulation in COMSOL Multiphysics:
- Draw the geometry within the COMSOL® software
- Import an external CAD file
- Use one of the LiveLink™ products
- Import mesh data from an external file
Each of these means of geometry creation provides different opportunities and advantages. The first method enables you to generate your geometry using only the COMSOL Multiphysics modeling environment. This method is the focus of today’s blog post, as we will discuss its associated workflow.
The general steps for creating a geometry include:
- Building geometry primitives corresponding to the model’s spatial dimension
- Using geometry operations (such as Boolean, partition, and transformation operations) to manipulate existing geometries to a new one
- Indicating how the software should deal with overlapping objects using Form Union or Form Assembly
Sometimes, it can be more efficient to create geometry primitives in lower dimensions using work planes and then extend them into the dimension that was not initially considered. Work planes can also be used to define cross sections from a higher dimensional entity to a lower dimensional workspace.
Let’s now dive further into the details of using geometry primitives, geometry operations, and work plane operations. Note that these operations can be used for geometries native to COMSOL Multiphysics as well as those created through another CAD program.
Using Geometric Primitives
COMSOL Multiphysics contains a number of ways in which you can generate the objects for your geometry. One option is to choose an object from the selection of built-in geometric shapes in the software, select and add the primitive object to your geometry sequence, and then edit the template provided through the Settings window. This enables you to specify the exact position, angle, and dimensions of the object as well as to quickly make changes to any of those settings, if needed. Once in the sequence, the object can then be combined and manipulated with other primitive objects to form your final geometry.
Creating and modifying a rectangle using the Settings window in COMSOL Multiphysics.
The types of objects available for you to choose from depend on the spatial dimension of your component. This includes geometric primitives for conventional shapes as well as other less traditional shapes. For 3D models, you can add objects like blocks or spheres as well as torus or helix objects. Similarly, for 2D models, primitives such as rectangles, circles, Bézier polygons, and parametric curves are available.
Another option for generating objects in your geometry sequence, available for 2D and 1D models, is to sketch geometric primitive objects with the mouse.
This is done by:
- Clicking on the respective button for the object you want to build
- Using the mouse in the Graphics window to click and define the center or corner of the object
- Dragging the mouse to generate the desired size and then clicking again
Immediately afterward, the object you have outlined appears and is added to your geometry sequence.
Creating and modifying a rectangle using the geometry drawing tools.
For 3D models, although you cannot sketch a geometry primitive with the mouse, you can draw a cross section of it in a work plane, which can then be expanded into a 3D object. We demonstrate both options mentioned above in dedicated chapters within the building 2D geometries part of the video series. Additionally, we discuss the advantages of using parameters during this process and demonstrate how they aid in streamlining your geometry setup.
Boolean, Transformation, and Partition Operations
After generating a few objects in your geometry sequence, you can start to combine them in meaningful ways using geometry operations. In the video chapters on building 2D geometries and 3D geometries in our series, we build a rectangular plate containing slots and a grille, respectively. This was done by using a combination of several Boolean and transformation operations.
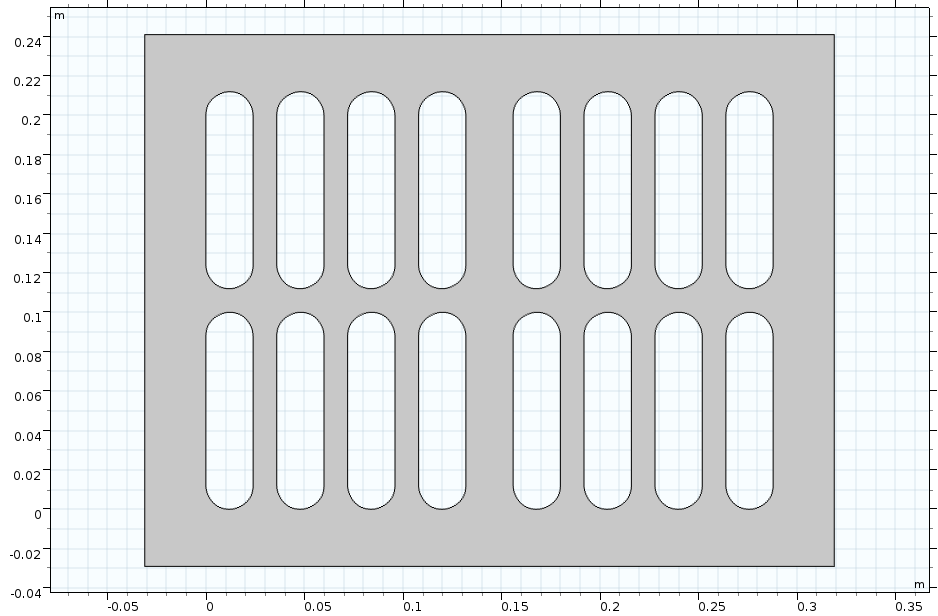
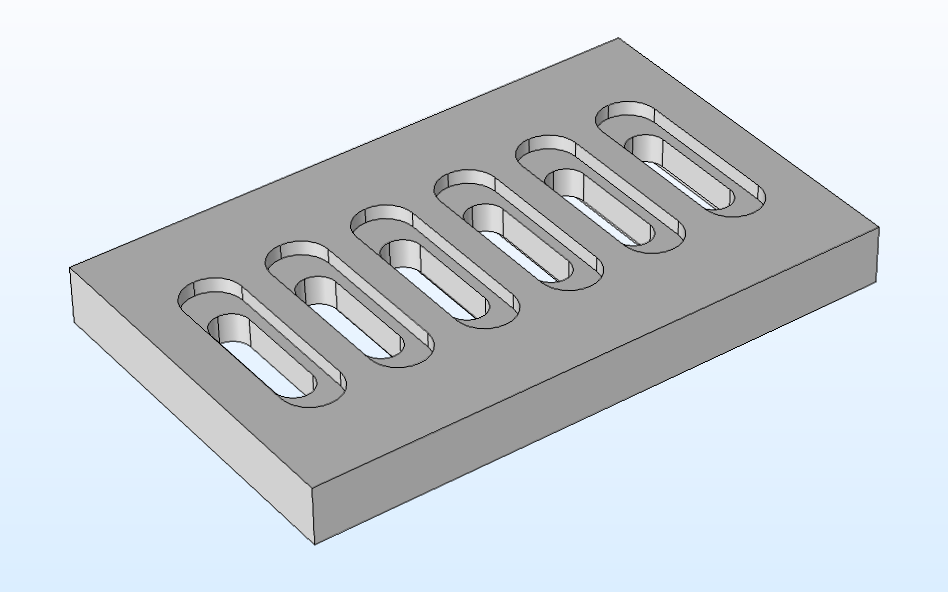
The rectangular plate with slots (left) and with a grille (right).
The Boolean operations used to create the geometries pictured above include the Union, Intersection, and Difference operations, which enable you to combine objects, create a new object from the intersection of other objects, and subtract objects from one another, respectively. Likewise, the transformation operations used include the Move, Copy, Mirror, and Array operations, which enable you to change the position of objects; create duplicate objects; reflect objects over a plane, line, or point; and create an arrangement of duplicates of another object.
Aside from some of the more conventional geometry features used above, there are also specialized geometry tools used to help create certain types of geometries. Partition operations enable you to split geometric entities such as objects, domains, boundaries, and edges so that you can separate, remove, or simplify the geometry in your model. When we discuss using partition operations for geometries in the video, we demonstrate how to perform this on a helix object as well as the geometry for the shell and tube heat exchanger tutorial model.
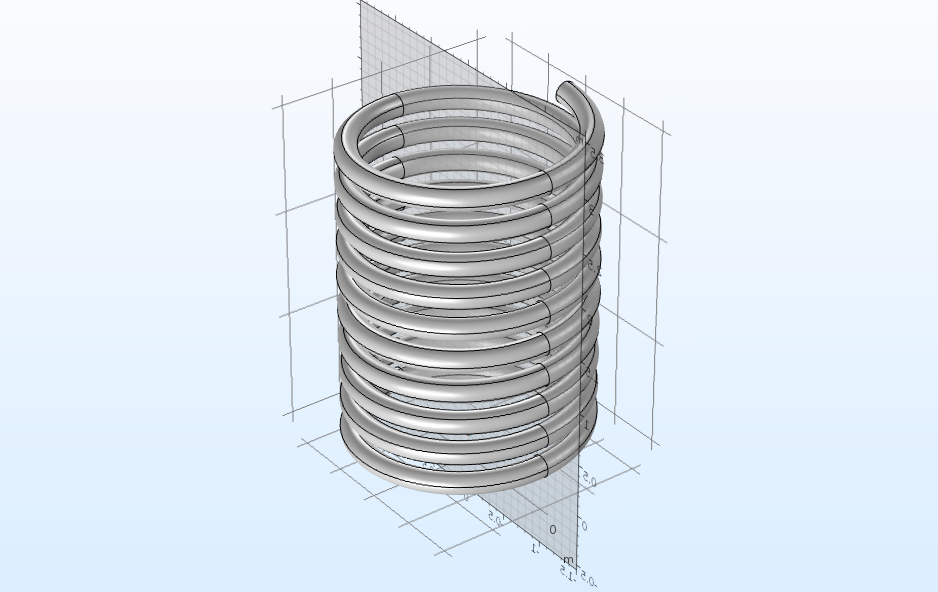
A helix geometry split down the middle, from our video chapter on partitioning geometries.
As you continue to build upon your geometry (adding more of these operations and other primitives to your sequence), you’ll notice that your sequence can become quite complex and that making any changes thereafter can become cumbersome. Changing the size of one object in the geometry may require other objects to be resized to accommodate that change. For these and other reasons, we encourage the use of parameters in the geometry operations you use in your sequence. We discuss the reasons for this and demonstrate how with a few of the example geometries built throughout the video series.
Work Plane Operations
COMSOL Multiphysics contains several tools known as work plane operations, which can be used to convert a 2D geometry in a work plane into a 3D object. In the video series, we show and demonstrate the Extrude, Revolve, and Sweep operations.
The Extrude operation enables you to extrude objects from a work plane or planar face to create 3D objects.
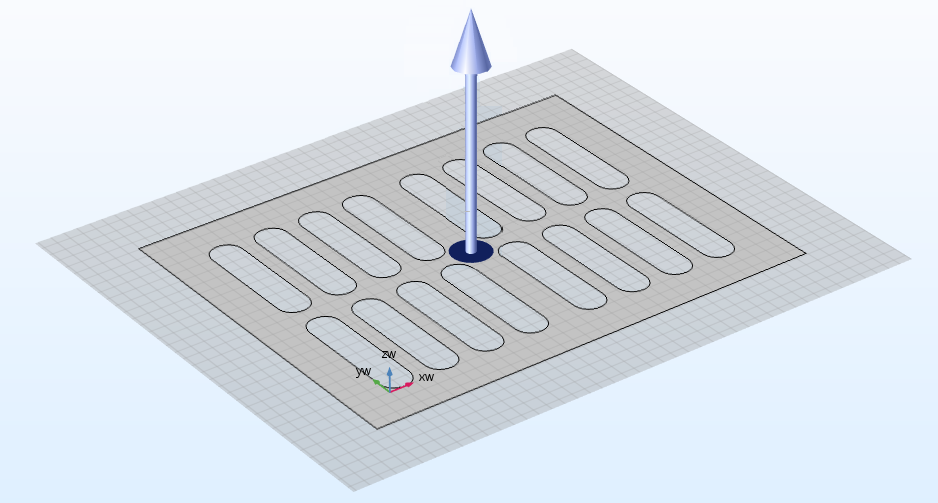
The Extrude operation, converting a rectangular plate with holes into a 3D block containing slots. The blue arrow in the center represents the direction in which the shape is extended, which is perpendicular to the work plane.
With the Revolve operation, you can revolve objects from a work plane or planar face about an axis to create 3D objects.
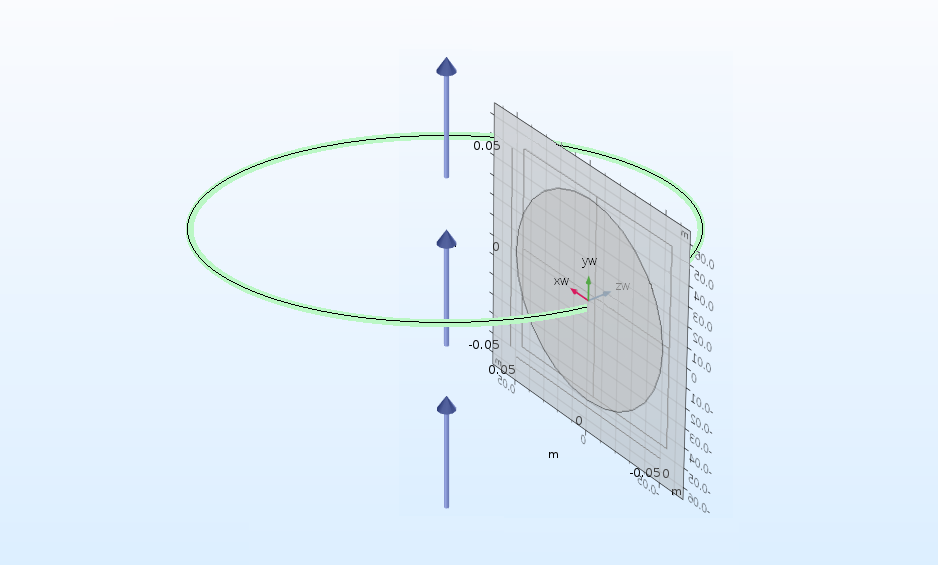
The Revolve operation, converting a circle into a torus. The blue arrows represent the axis about which the shape is revolved.
Finally, there’s the Sweep operation, which enables you to sweep objects from a work plane or planar face along a path to create a 3D object.
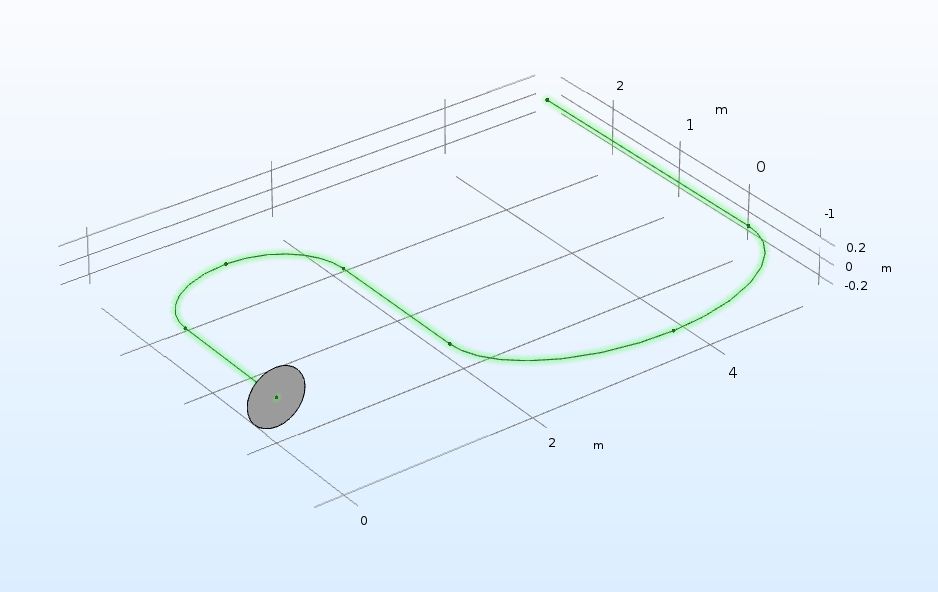
The Sweep operation, converting a circle and 2D line path into a pipeline. Two work planes that are perpendicular to each other are used to define the shape and line path separately.
Using these work plane operations (starting from a 2D model and then expanding it into 3D) can be a significantly quicker alternative for building your 3D geometry, as opposed to building it entirely of 3D objects.
Cross Section Geometry Operation
The COMSOL Multiphysics software also contains a tool for converting a 3D geometry into a 2D geometry. This is done through using a work plane along with the Cross Section geometry operation. The functionality can be used to simplify your model, among other things, which we discuss in the video series.
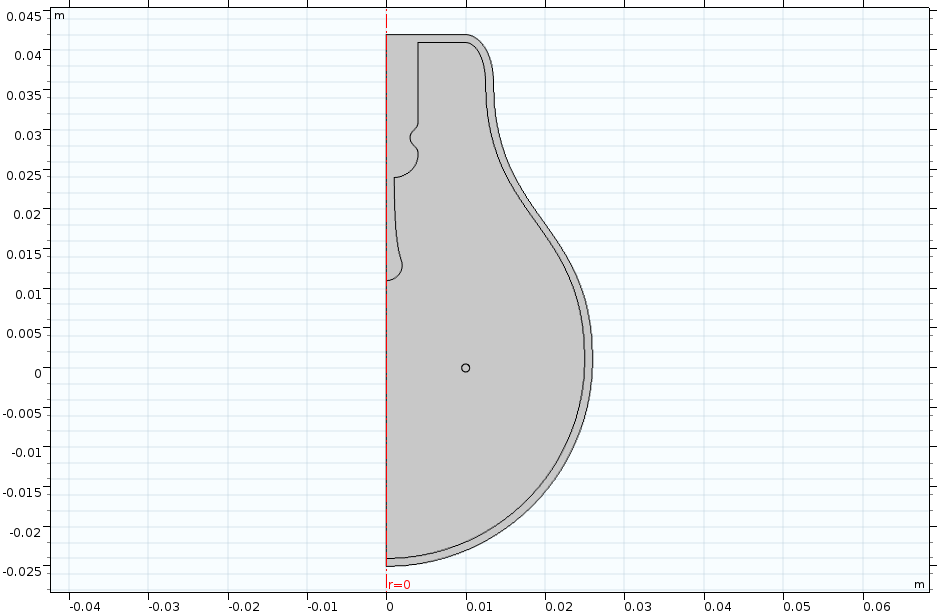
The axisymmetric cross section of a light bulb, built in the video chapter on creating 2D models from 3D geometries.
The geometry generated through the Cross Section operation is based on the intersection of your 3D geometry with a work plane. Thus, the 2D geometry you obtain is the result of wherever the work plane cuts through the 3D solids in your model. Within the operation, you can choose for the work plane to intersect (and thus include) all objects or a selection of objects that you specify.
To obtain the appropriate cross section for your analysis, using this functionality may require performing some additional preparation on the original 3D geometry. Sometimes, this means separating and then removing certain parts of your geometry, wherein partition operations can be helpful. We elaborate on this further and demonstrate it in a dedicated chapter within the video series.
Next Step: Watch the Introductory Video Series on Using Geometry Tools
Whether you are building a geometry entirely within COMSOL Multiphysics or working off of an external file, you can use the geometry functionality discussed in this blog post to completely customize the composition of your geometry objects. If you are interested in seeing these tools in action, watch our introductory geometry video series:




Comments (2)
Kyle Walton
October 27, 2017Are there any strategies or conventions when trying to build more complicated geometries within COMSOL? I have had some success in building the some geometries, but they are pretty much unmanageable.
Amelia Halliday
November 3, 2017Hello Kyle, if you look through our blog posts that fall under the Geometry category (https://www.comsol.com/blogs/category/all/geometry/) you can see several examples of geometries created with varying levels of complexity.
Additionally, many of the models in the Application Gallery (https://www.comsol.com/models) provide step-by-step instructions in the PDF files as to how to create the geometry used in the model, including any specific modeling strategies that were used.