The Gaussian beam is the most popular light source in wave optics. This blog post discusses the evanescent component of the nonparaxial Gaussian beam background field, a feature available in the Electromagnetic Waves, Frequency Domain interface in the Wave Optics and RF modules as of version 5.5 of the COMSOL Multiphysics® software.
Introduction to Paraxial and Nonparaxial Gaussian Beams
The Gaussian beam is one of the electromagnetic beams that focuses into the smallest possible spot. When the focusing angle is small, it’s called the paraxial Gaussian beam, whereas it’s referred to as the nonparaxial Gaussian beam if it focuses more tightly.
The paraxial Gaussian beam has a longer history and is well defined by the paraxial theory by Kogelnik and Li (refer to Ref. 1 for the paraxial theory and Ref. 2 for the paraxial formulas). On the other hand, the theory for the nonparaxial Gaussian beam is not as handy (Ref. 3).
COMSOL introduced the nonparaxial Gaussian beam background field as of version 5.3a. This formulation is a better approximation than using the paraxial Gaussian beam for nonparaxial cases. The formulation of the nonparaxial Gaussian beam consists of two parts:
- The propagating component
- The evanescent component
Version 5.3a includes the propagating component, and as of version 5.5, the formulation is full fledged; i.e., it includes the evanescent component. This component computes a small portion of the field, which is important for highly nonparaxial Gaussian beams.
Angular Spectrum Formulation
We already discussed the derivation of the nonparaxial Gaussian beam based on the angular spectrum method. The description was a general introduction to the nonparaxial formulation. In this blog post, we are going to talk about the formulation with a little more practicality.
Let’s consider the full vector field, in which the propagation direction is the z-axis. There are various different representations depending on how the polarization is chosen. There are at least three reference papers (Ref. 3–5) that show apparently different mathematics, but the essential points are the same for all. In this blog post, we follow Chaumet’s formulation, which is the simplest and easiest to understand. For the half-space (that is, z>0) it follows that
where k_0^2=(\omega/c)^2 = k_x^2+k_y^2+k_z^2 and A_i(k_x,k_y), i=x, y is called the angular spectrum function, and the polarization is determined by E_{x,0} and E_{y,0}.
It is easy to confirm by hand calculation that this field automatically satisfies the Helmholtz equation and the Maxwell equations (Gauss’ law). Also, it is easy to see that this formulation can take arbitrary integrable functions for the angular spectrum function.
As described in the previous post, this formulation represents a three-dimensional picture of the plane waves propagating at various angles to form a Gaussian beam. The main propagation direction is the z-axis so that the propagation angles of the plane waves are characterized by the projection of \vec{k}_0 onto the transverse plane; i.e., the xy-plane, which is \vec{k}_x and \vec{k}_y. Summing up all of the plane waves means the integration with respect to k_x and k_y.
For Gaussian beams, the angular spectrum function is conventionally chosen in the focal plane and assumed to be a Gaussian profile; i.e.,
This angular spectrum function implies that many waves are at a near-zero angle, which is the z-axis, and the higher-angle contribution tapers off as the angles increase. Here, we note that the integration for each k_x and k_y ranges from -\infty to +\infty. The majority of the contribution of the integration comes from the range from -k_0 to k_0. This solution is called the propagation component. (This is what was added as of version 5.3a.)
Mathematically, the Maxwell equations accept the other solution: the contribution from the integration range from k_0 to +\infty and from -k_0 to -\infty as well. This solution is called the evanescent component. This is the feature that was added as of version 5.5. What happens in this case is, where k_x=k_0, k_y=k_0 for example, it follows that k_z^2 = k_0^2 – k_x^2-k_y^2 = -k_0^2. So, k_z = ik_0. Substituting this into the above formulas, we get the factor \exp[-k_0z], which decays quickly as the field propagates far from the focus; i.e., z=0. So, it’s a tiny portion compared to the propagating component. Dropping off this component is still a good approximation of the nonparaxial Gaussian beam, but it can become nonnegligible as the focusing angle gets higher.
Simulation of a Nonparaxial Gaussian Beam in COMSOL Multiphysics®
In the physics node, you can see the settings for defining the nonparaxial Gaussian beam background field. There are a couple of things that we have to be aware of.
No Perfect Transverse Mode
First of all, it is known that there is basically no perfect transverse mode for nonparaxial Gaussian beams near the focal plane, except for out-of-plane cases in 2D. This is because there is always some small amount in the longitudinal component. From this fact, the definition of the polarization of the field is no longer clear.
Let’s look at the screenshot below. This is an example of the settings for an in-plane nonparaxial Gaussian beam propagating along the x-axis in 2D. Even if you choose the amplitude of the Gaussian beam as (0,1,0), there will be the x-component electric field. Regardless of your settings, COMSOL Multiphysics will try to solve the Maxwell equations and it will output necessary longitudinal components, if any.
Aliasing
The above formulation contains integrations. In implementing these formulas in COMSOL Multiphysics, all of these mathematical operations have to be digitized and processed numerically. There arises a sampling issue called aliasing where you get artifacts if the sampling number is not large enough. The Wave vector count and the Maximum transverse wave number settings are relevant to this issue. If Automatic doesn’t work, you may want to tweak these two numbers.
The Wave vector count defines how many different angles you want to propagate your plane waves with instead of a continuously infinite number of angles. In the below settings, 51 angles are selected instead of an infinitely large number. This is large enough for 2D, but be careful in 3D cases, as it will freeze your simulation, since in 3D the total wave number count is the square of the Wave vector count.
The Maximum transverse wave number defines how much you allow for the imaginary longitudinal wave number. For example, if you choose 2*ewfd.k0 for the transverse wave number, as in the screenshot below, you will get k_x^2 = k_0^2- k_y^2 = k_0^2 – 2k_0^2 = -k_0^2. In this case, it’s 2D, so the transverse wave number is k_y and the longitudinal wave number is k_x. This setting means that you allow for k_x to be from 0 up to \pm ik_0 in addition to the propagating component for the range of -k_0 \le k_x \le k_0. The evanescent component is basically small. So, 2*ewfd.k0 is enough in many cases.
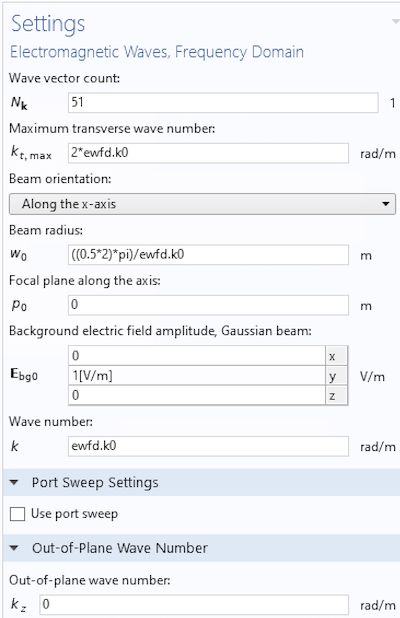
Screenshot for the evanescent wave setting for a 2D model.
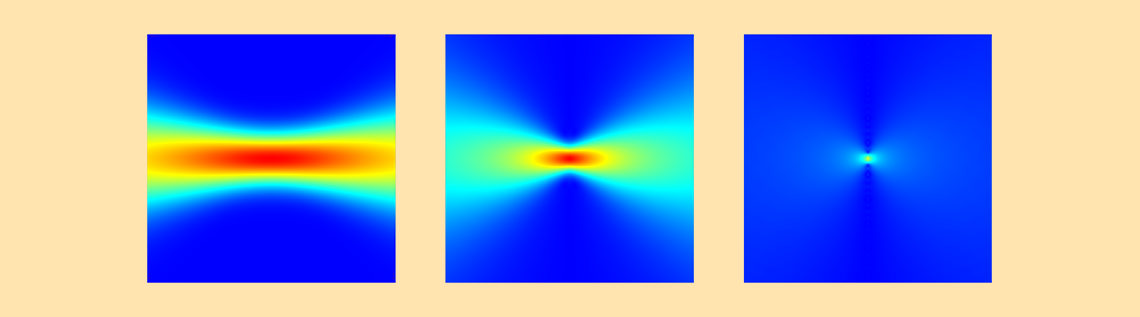
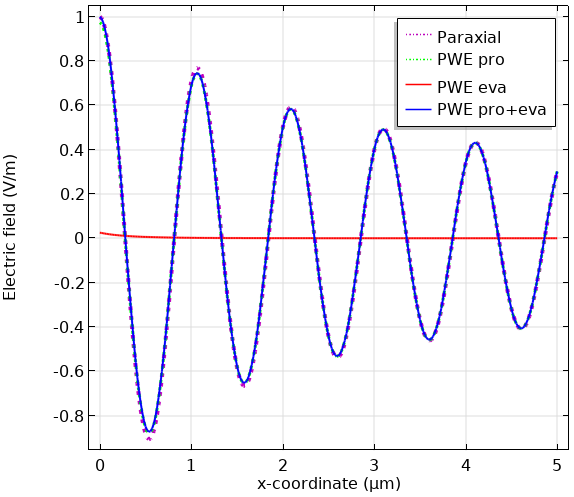
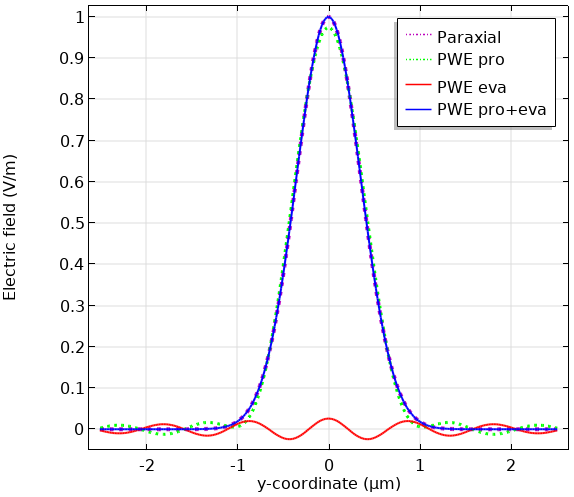
The following is a comparison between the paraxial plane wave expansion with a propagating component (PWE pro), plane wave expansion with an evanescent component (PWE eva), and plane wave expansion with propagating and evanescent components (PWE pro+eva) for the waist radius of 0.5 \lambda, which is highly nonparaxial. The first surface plots are the norm of the field. For PWE eva and PWE pro+eva, it shows only the positive half space because it’s defined in the half space. The line plots are x– and y-profiles of the field. These plots show that the difference between the paraxial and nonparaxial Gaussian beams takes place near the focal plane in the transverse direction.

Comparison of the electric field norm calculated by each method: paraxial approximation, plane wave expansion (propagating component), plane wave expansion (evanescent component), and plane wave expansion (propagating and evanescent components).
Comparison of the electric field in x and y axes calculated by each method: paraxial approximation, plane wave expansion (propagating component), plane wave expansion (evanescent component), and plane wave expansion (propagating and evanescent components).
The last surface plots are the error from the Helmholtz equation (refer to the previous post for the definition of the error). These plots are more impressively expressing the improvement of the solution’s rigorousness to the Helmholtz equations.

Comparison of the error magnitude from the Helmholtz-compliant solutions calculated by each method: paraxial approximation, plane wave expansion (propagating component), plane wave expansion (evanescent component), and plane wave expansion (propagating and evanescent components).
Concluding Remarks
By adding the evanescent component to the nonparaxial Gaussian beam background field feature, it’s now in full formulation that contains all possible rigorous solutions to the Maxwell equations. As seen in the above profile plots, the paraxial Gaussian beam formula looks surprisingly correct for the nonparaxial regime. However, if we look at the error plot, it’s obvious that it doesn’t satisfy the Helmholtz equation in a domain for highly nonparaxial cases. This is why we need a rigorous formulation for nonparaxial Gaussian beams.
References
- H. Kogelnik and T. Li, “Laser beams and resonators”, Applied Optics, vol. 5, no. 10, pp. 1550–1567, 1966.
- “Gaussian beam”, Wikipedia, https://en.wikipedia.org/wiki/Gaussian_beam.
- P.C. Chaumet, “Fully vectorial highly nonparaxial beam close to the waist”, JOSA A, vol. 23, no. 12, pp. 3197–3202, 2006.
- R. Martinez-Herrero, P.M. Mejias, and A. Carnicer, “Evanescent field of vectorial highly non-paraxial beams”, Optics Express, vol. 16, no. 5, pp. 2845–2858, 2008.
- P. Varga and P. Török, “The Gaussian wave solution of Maxwell’s equations and the validity of scalar wave approximation”, Optics Communications, vol. 152, no. 1–3, pp. 108–118, 1998.






Comments (3)
Harek Tarek
May 20, 2020I’m interested in this
Alexander Kildishev
June 13, 2020Thank you, Yousuke! A very important development for nano-optics.
Peng W
April 17, 2021Dear Mr. Yosuke Mizuyama,
I’ve watched a webinar given by you with the topic of ‘Simulating Optical Waveguides with COMSOL Multiphysics’. In that webinar you mentioned an example of simulating ‘tapered waveguide’. I’d just like to ask if there is a mph file for this simulation. Recently, I was doing simulation on grating couplers. I’m not sure about the correct way to excite a proper mode before the light enters the grating region. I think that is very similar to the case of ‘tapered waveguide’ where the refractive index along the longitudinal direction is not constant. Therefore, it would great if I could have an example mph file of the tapered waveguide as a reference. I’ve tried to find it on COMSOL’s website but failed. So I’m wondering if that’s just an demonstrative file created by you and hasn’t been uploaded onto the website? Looking forward to your reply. Thanks.
Best regards