Simulating fluid flow underground or in other porous media is common in a number of engineering fields, such as agricultural, chemical, civil, and nuclear engineering. To help engineers and scientists simulate different types of porous media flow, the COMSOL Multiphysics® software provides a comprehensive set of physics interfaces. Today, we will go over the various interfaces that you can use and discuss how to choose the best one for your application.
Modeling Microscopic Flow on a Macroscopic Scale
In the 19th century, a French engineer named Henry Darcy pioneered the study of fluid flow through porous media. When conducting experiments on sand, he found that the flow rate of the fluid in a porous medium is proportional to the hydraulic force applied to it. This later became known as Darcy’s law.

An experiment of capillary flow through a porous medium (brick). Image by Hankwang — Own work. Licensed under CC BY-SA, via Wikimedia Commons.
Modeling porous media flow on a macroscopic scale involves numerically solving Darcy’s law, including later extensions such as the Brinkman equations. Even though it’s possible to simulate porous media flow on the microscopic level, such as in this pore-scale flow example, the macroscopic approach is more efficient. This approach neglects the detailed structures of pores and represents the porous medium’s properties through two key macroscopic quantities: porosity and permeability. This significantly reduces the computational cost. We’ll be focusing on the macroscopic approach in today’s blog post.
Choosing the Correct Porous Media Flow Interface in COMSOL Multiphysics®
COMSOL Multiphysics offers several physics interfaces to model porous media and subsurface flow. In this section, we use an example of a riverbank to help explain these interfaces and how to choose between them.
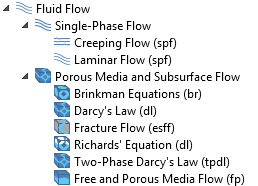
The model tree, displaying the porous media and subsurface flow interfaces.
Now, let’s imagine there is a river flowing through the countryside on a sunny day, as pictured below. In our example, the river saturates the soil in the riverbank, which contains a deep fracture. A water table divides the riverbank into two zones, a phreatic zone that is fully saturated with water and a vadose zone that is unsaturated.
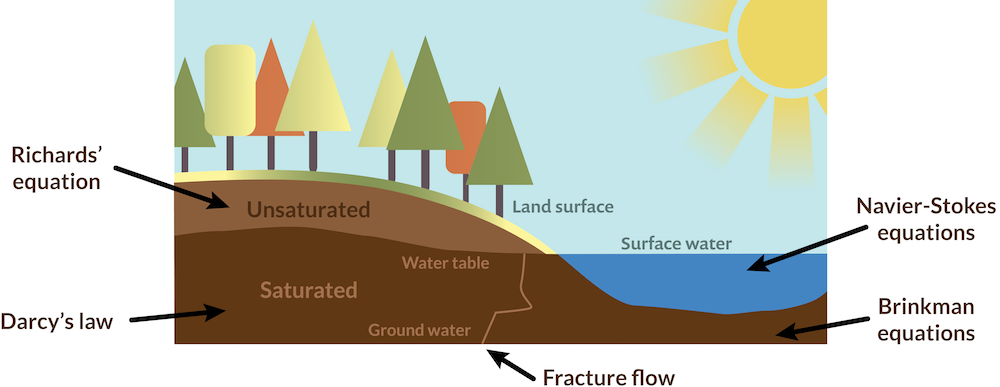
Cross-sectional view of a riverbank and the governing equations applied to each flow regime.
Let’s take a look at each flow regime and its applicable physics interface.
Free Flow: The Navier-Stokes Equations
The fluid flow in the river channel is governed by the Navier-Stokes equations. Depending on the Reynolds number, you can model this section by choosing one of the single-phase flow interfaces (for example, the Laminar Flow interface). These interfaces compute both velocity and pressure.
Fast Flow in Porous Media: The Brinkman Equations Interface
The subsurface flow in the hyporheic zone near the streambed is typically described by the Brinkman equations. The Brinkman equations account for fast-moving fluids in porous media with the kinetic potential from fluid velocity, pressure, and gravity driving the flow. These equations extend Darcy’s law to describe the dissipation of the kinetic energy by viscous shear, similar to the Navier-Stokes equations. Therefore, the Brinkman Equations interface is well suited for modeling fast flow in porous media, including transitions between slow flow in porous media governed by Darcy’s law and fast flow in channels described by the Navier-Stokes equations. The Brinkman Equations interface computes both the velocity and pressure.
Note that the Free and Porous Media Flow interface solves the Brinkman equations in the porous domains and Navier-Stokes equations in the fluid domains. Alternatively, you can add a Laminar Flow interface and turn on Enable porous media domains, which gives you the same underlying equations as the Free and Porous Media Flow interface.
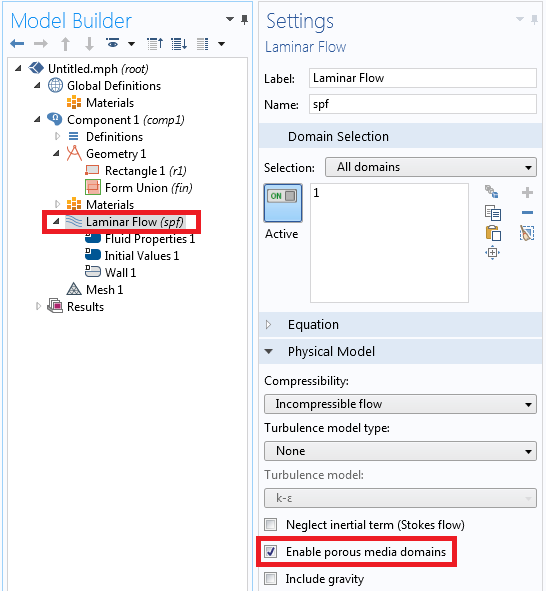
Settings showing the Enable porous media domains option in the Laminar Flow interface, which solves the Brinkman equations in the porous domains.
In our Forchheimer Flow tutorial model, the flow is described by the Navier-Stokes equations in the free region and the Brinkman equations in the porous region.

The Forchheimer Flow tutorial model, which demonstrates how to couple the fluid flow in an open channel and an attached porous block.
Slow Flow in Porous Media: The Darcy’s Law Interface
Darcy’s law describes fluid movement through interstices in a fully saturated porous medium that is mainly driven by a pressure gradient. We can use the Darcy’s Law interface to model water moving in an aquifer or streambank. In a porous medium, pore walls impede momentum transport to the fluid outside of the individual pores. Thus, the transport of momentum due to shear stresses in the fluid is negligible. While the Darcy’s Law interface only computes pressure, the velocity field is then determined by the pressure gradient, fluid viscosity, and permeability.
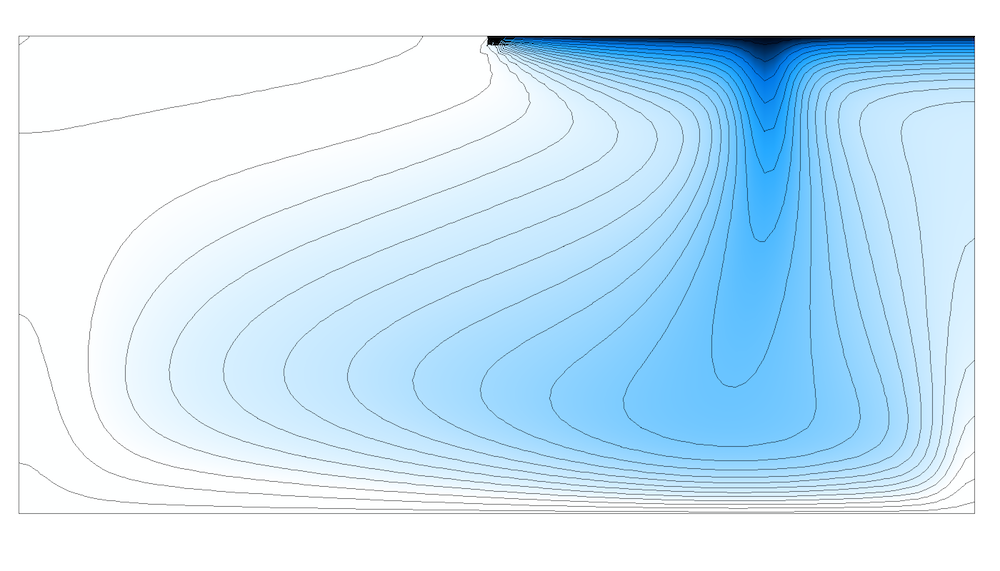
The Elder problem examines buoyancy flow in a porous medium by coupling the Darcy’s Law and Solute Transport interfaces.
Variably Saturated Porous Media: The Richards’ Equation Interface
So far, all of the governing equations that we’ve discussed assume that the porous medium is fully saturated, whereas the Richards’ equation describes the movement of water in unsaturated soils. Therefore, we can use the Richards’ Equation interface to model partially saturated porous media, such as the fluid’s movement in the riverbank near the water table.

We can use the Richards’ equation to examine the saturation level in variably saturated soils, as in this tutorial model.
This interface accounts for the changes in hydraulic properties as fluids move through the medium, filling some pores and draining others. Fluid retention models (the van Genuchten or Brooks-Corey models, for example) are built into this interface. Similar to the Darcy’s Law interface, only pressure is computed in the Richards’ Equation interface. The Richards’ equation is nonlinear due to the fact that the hydraulic properties vary based on saturation, which can make it challenging to compute numerically.
Flow Along Surfaces: The Fracture Flow Interface
We can use the Fracture Flow interface to simulate flow in fractures within a solid or porous medium. In this interface, Darcy’s law is solved along the surface (or along a line in 2D simulations). Flow in fractured porous media typically moves faster along the fractures. It can also flow through the tiny pores within the surrounding matrix blocks at a much slower velocity. Therefore, the Fracture Flow interface can be coupled with the Darcy’s Law or Richards’ Equation interface. This is demonstrated in the Discrete Fracture tutorial, which couples fracture flow with Darcy’s law in the porous domain.
Two-Phase Porous Media Flow: The Two-Phase Darcy’s Law Interface
Studying two-phase porous media flow, such as in oil reservoirs, is often of interest to those in the petroleum industry. To simulate this concept, we can use the Two-Phase Darcy’s Law interface, which extends the Darcy’s Law interface. In addition to calculating pressure, the Two-Phase Darcy’s Law interface solves a transport equation for the fluid content of one fluid phase. Fluid properties, such as density and viscosity, are averaged based on the saturation and properties of each phase.
Which Interface Do I Choose?
In the following table, we summarize the available porous media flow interfaces. See the product specification chart for more details about the required add-on modules for each interface.
| Physics Interface | Flow Regime | Equations Solved For |
|---|---|---|
| Laminar Flow interface | Free flow | Navier-Stokes equations |
| Laminar Flow interface with the Enable porous media domains option | Free flow and fast flow in porous media |
|
| Free and Porous Media interface | Free flow and fast flow in porous media |
|
| Brinkman Equations interface | Fast flow in porous media | Brinkman equations |
| Darcy’s Law interface | Slow flow in porous media | Darcy’s law |
| Richards’ Equation interface | Variably saturated porous media | Richards’ equation |
| Fracture Flow interface | Flow along surfaces of fractures | Darcy’s law |
| Two-Phase Darcy’s Law interface | Two-phase flow in porous media |
|
Concluding Thoughts on the Porous Media and Subsurface Flow Interfaces
In this blog post, we discussed the different porous media and subsurface flow interfaces available in COMSOL Multiphysics. You can also easily couple these interfaces with other physics to study poroelasticity, geothermal processes, pesticide runoff, aquifer characterization, and more.
To discuss how the COMSOL® software can help you address your specific fluid flow modeling needs, contact us using the button below.
Are you a COMSOL Multiphysics user with a question about modeling porous media flow? Feel free to contact our Technical Support team.




Comments (6)
Ivar Kjelberg
February 15, 2017Thanks for a clear explanation, PLS make more of these BLOGs, as there are plenty of domains where several models prevail, but when and which to use for each case, is not always easy to sort out 🙂
Yige Zhang
May 15, 2017Thank you for the nice explanation.
Has the option “Enable porous media domains” been removed?
I cannot find it in my “Laminar Flow interface” in version 5.2a. Since which version the option was removed?
Supriya Upadhyay
May 19, 2017Hi.. I am working on a case where there are three domains (all rectangles), the middle one has marangoni convection and the bottom domain is porous. The difficulty that I am facing is having these two physics simultaneously. The flow is under microgravity. I have used laminar flow and heat transfer in fluids with enable porous media option and a weak contribution on the right boundary of the second domain for marangoni flow. Could you please suggest me a way as to how I can use these physics simultaneously? The fluid and porous medium are both Al-Si alloy!
Otherwise, with a view of having mutiple physics, different for different domains, which out of darcy, brinkman or forchheimer equations should I use? Using any of these requires velocity as an input and in my case, the marangoni velocity from second domain serves as an input velocity to the bottom porous domain..
Any help in this regard shall be highly appreciated..Thanks!!!
Caty Fairclough
June 7, 2017Hi Yige and Supriya,
Thanks for your comments and interest in this blog post.
For your questions, please contact our Support team.
Online Support Center: https://www.comsol.com/support
Email: support@comsol.com
farzad forouzanfard
November 3, 2017Thanks for this nice post, I have a question, can we use brinkman’s equation to calculate upstream’s slope safety factor of an earth fill (or embankment) dam in rapid draw down conditions? because in rapid draw down condition the reservoir discharge in a short time and the velocity of fluid in porous materials is relativity high.
Matej Cerny
December 22, 2017Does Comsol use concept of real flow velocities? I’ve tried trial version of darcy flow + heat transfer, and the value of porosity doesn’t affect the evolution of temperature field.